Your job in this assignment is to prepare programs to solve each of the given problems.

problem 1: prepare a GraphicsProgram subclass which draws a pyramid comprising of bricks arranged in horizontal rows, so that the number of bricks in each row reduces by one as you move up the pyramid, as shown in the given sample run:

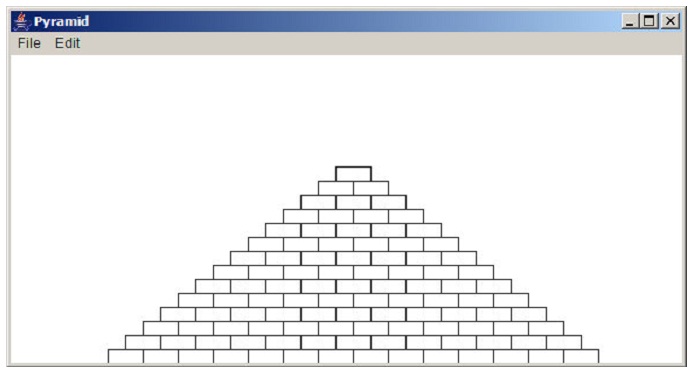
The pyramid must be centered at the bottom of the window and must use constants for the given parameters:

BRICK_WIDTH: The width of each brick (30 pixels)
BRICK_HEIGHT: The height of each brick (12 pixels)
BRICKS_IN_BASE: The number of bricks in the base (14)

The numbers in parentheses show the values for this diagram; however you should be able to change those values in your program.

problem 2: Assume that you have been hired to produce a program which draws an image of an archery target - or, if you prefer commercial applications, a logo for a national department store chain - that looks like this:

This figure is simply three GOval objects, two red and one white, drawn in the correct order. The outer circle must have a radius of one inch (72 pixels), the white circle consists of a radius of 0.65 inches, and the inner red circle has a radius of 0.3 inches. The figure must be centered in the window of a GraphicsProgram subclass.

problem 3: prepare a GraphicsProgram subclass which draws a partial diagram of the acm.program class hierarchy, as shown:

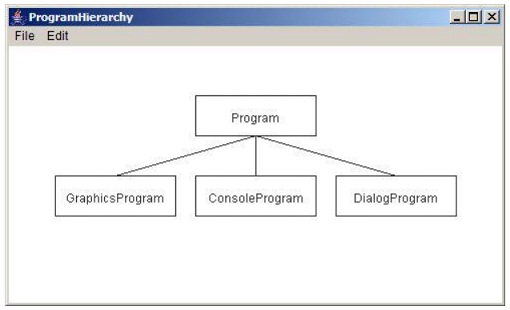
The only classes you require to create this picture are GRect, GLabel, and GLine. The main part of the problem is specifying the coordinates so that the different elements of the picture are aligned properly. The aspects of the alignment for which you are responsible are:

• The width and height of the class boxes must be specified as named constants so that they are easy to change.

• The labels must be centered in their boxes. You can find out the width of a label by calling label.getWidth() and the height it extends above the baseline by calling label.getAscent(). If you want to center a label, you require to shift its origin by half of these distances in each direction.

• The connecting lines must begin and end at the center of the suitable edge of the box.

• The whole figure must be centered in the window.

problem 4: In high-school geometry, you learned the Pythagorean Theorem for the relationship of the lengths of the three sides of a right triangle:

a² + b² = c²

This can alternatively be written as:

c = √a² + b²

The one piece that is missing is taking square roots that you can do by calling the standard function Math.sqrt. For illustration, the statement:

double y = Math.sqrt(x);
sets y to the square root of x.

prepare a ConsoleProgram which accepts values for a and b as ints and then computes the solution of c as a double. Your program must be able to duplicate the given sample run:

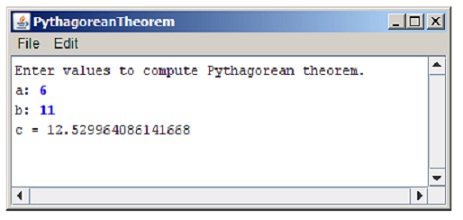
problem 5: prepare a ConsoleProgram which reads in a list of integers, one per line, until a sentinel value of 0 (which you should be able to change easily to some other value). When the sentinel is read, your program must display the smallest and largest values in the list, as illustrated in this sample run:

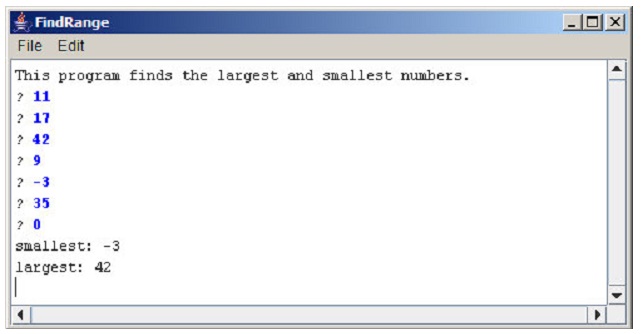
Your program must handle the given special cases:

• If the user enters only one value before the sentinel, the program must report that value as both the largest and smallest.

• If the user enters the sentinel on the very first input line, then no values have been entered and your program must display a message to that effect.