problem1)
prepare a C function to solve the system of linear equations A x = y where A is an N by N matrix in the format of pointer-to-pointers and y is a vector in the format of a pointer. The function should return a pointer to the answer vector x . Your function should have the prototype:
double *Gaussian(double **,double *, int).
The function should implement the Gaussian Elimination Algorithm with Partial Pivoting.
Test your function on the system:

problem2)
Amend your Gaussian elimination function to solve for multiple right hand sides (Simultaneous systems of equations). The prototype should be
double **GaussianS(double **,double **,int,int)
where the fourth argument is the number of right hand side vectors.
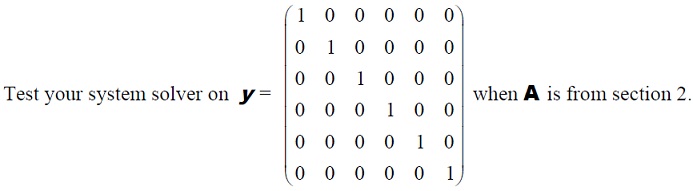
What is x ?
problem3) prepare a C function with prototype: double **Inverse(double **,int) to find the inverse of a matrix. Find the inverse of matrix A.
problem4)
Speed in scientific computing is measured in megaflops, gigaflops, teraflops and petaflops. A megaflop is 106 floating point arithmetic operations (+, -, *, /) in one second What are a gigaflop, a teraflop and a petaflop? To determine the real megaflop rate of a given algorithm on a given computer you must first determine theoretically the total number of Floating point arithmetic operations the algorithm takes and then divide that by 106 times the total time taken to run the algorithm. Determine the speed of your matrix inverse function by timing how long it takes to invert a random matrix (you should use the function given in lecture to generate a random square matrix) of size N, where N takes the integer values:
i. 2 < =N < =50, (~50 values)
ii. N = {55, 60, 65, … 200} (~30 values in increments of 5)
iii. N = {225, 250, 275, … 1000} (~30 value in increments of 25)
iv. N = {1200, 1400, …,2000} (~10 values in increments of 200)
Plot Megaflops vs. ln2(N). {You may use Excel, Maple or any plotting package.}
problem5)
Loop order, the exact form of the pointer and index arithmetic and the compiler and option flags set at compile time all can influence the speed of that a code runs. Experiment with improving your code’s running speed for the N=1000 Matrix Inverse case by trying variations of these. Rerun all of the cases from Section 4 using your new faster code. Insert OpenMP #pragma instructions. By what factor is your ‘best’ code faster than the ‘naive’ code your first wrote? The Intel MKL Library contains special routines to do common Numerical Linear Algebra tasks. It implements a Library called LAPACK efficiently. If you use the appropriate Intel MKL Lapack routines, how much does this speed up your code?
Time your fastest possible matrix inverse function. If you know that the right hand side of a set of simultaneous equations take the form of an identity matrix, what steps can to take to exploit this fact to reduce the total number of operations you must perform to find out the matrix inverse. Can you quantify the savings for a general N by N Inverse. Can you see these savings in reduced execution times? Produce timings for the set of matrix sizes used in Sections 4 above. Plot the results for running your fastest matrix inverter on one of the PCs in rooms 414 & 410 on one graph. If you have access to any other computer, include the speed curves for those machines on your graph as well. Can you describe the shapes of the curve?
problem6) The real discrete cosine transform (DCT) represents the data xi at N+1 discrete points as the sum of N+1 cosine functions of amplitude yj:
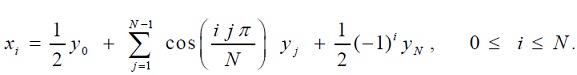
This relation may be thought of as a matrix linear equation: CN y’ = x , where x and y’ are vectors of size N+1 such that x = [ x0, x1, …,xN-1 , xN ] and y’ = [ ½ y0, y1,… ,yN-1 ,½ yN ], (or x = CN’ y ) {Note the notational convention to distinguish normal vectors x and vectors with their first and last entries halved: y’ } and CN is an N+1 by N+1 matrix whose i+1, j+1 th element is cos(ijπ/N). CN’ has entries of ½ down its first column and entries of (½ , -½, ½, -½, ….) down its last column. Solve the linear system CN’ y = x , when x = (0, 1, 2, 3, 4, 5, … , N) for N = 64, 256 & 1024. Not counting the time it takes to generate the CN’ matrix, how long does your code take for each of these three systems? How accurate are your answers?