problem 1: Why are homogeneous co-ordinates used in computer vision? What is the use of homogenous co-ordinates makes possible in terms of camera models. 

problem 2: Consider the case where a point P = (X,Y,Z) projects to the image plane. Using the matrix below which defines the projection of this point for a camera with focal length f to prove that every other point on the line from the origin through the point P projects to the same image point.

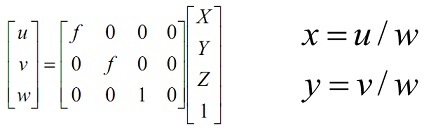
problem 3: A 3d rotation matrix has 9 (3 by 3) entries, and a 2d rotation matrix has 4 (2 by 2) entries. How many actual degrees of freedom are there in a 3d or 2d rotation? In other words, what is the minimum number of parameters necessary to uniquely specify a 3d rotation and a 2d rotation (answer with 2 numbers)? What does this imply about the relationship between the entries of a rotation matrix?
 
problem 4: What is the time complexity of a convolution with an n by n sized kernel when using a direct convolution with a 2d mask, and when using a separable kernel. Each of the answers is in the form of O(?) where ? is an expression in n.

problem 5: A square in the 2d plane has the x and y co-ordinates of (0, 0), (1, 0), (0, 1) and (1, 1). Apply a scaling of 0.5 units in the x direction, followed by a translation of three units in the x direction and three units in the y direction. First prepare down this transformation in homogeneous co-ordinates, and then apply it to the four corners of the square. Then prepare the new x and y co-ordinates of the four corners.