problem1) Velocity profile for laminar flow in round pipe is given by the equation u(r)=umax[1−(r/R)2] where Umax is the centerline velocity, R is the pipe radius and r is the radial distance from the pipe centerline.
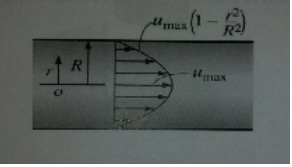
a) Determine the velocity gradient at the pipe wall? Note that normal distance from the pipe wall is y=R-r, thus dy=-dr and du/dy=-du/dr.
b) what is the shear stress at pipe centerline?
c) Demonstrate that the velocity gradient, and as the shear stress varies linearly from zero at the pipe centerline to a maximum at the pipe wall.
problem2) Determine the equal annual payment series that will be equivalent to the following increasing series of payments if the interest rate is 12%
(a) compounded annually;
(b) compounded continuously.
$600 at the end of the first year
$800 at the end of the second year
$1,000 at the end of the third year
$1,200 at the end of the fourth year
$1,400 at the end of the fifth year
$1,600 at the end of the sixth year
$1,800 at the end of the seventh year