Questions -

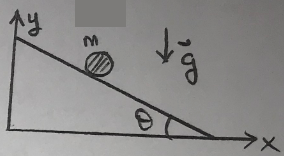
Q1. A particle of mass m slides on a smooth inclined plane under the uniform gravitational field. Using d'Alembert's principle, obtain the equation of motion.

Q2. Consider the following spring-mass system on a smooth horizontal surface.

If x₁ and x₂ are measured from their (M₁, M₂) equilibrium positions, write down the tagrangian of the system and obtain equations of motion.

Q3. The point of a support a simple pendulum of mass m and length l connected to a spring of spring constant k and constrained to move in y-direction.

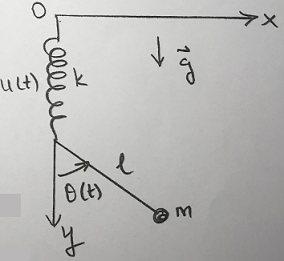
Using the covariant form of Newton's second law, d/dt (∂T/∂q^·_i) - ∂T/∂q_i = Q_i, where Q_i = _j=1∑ⁿ t^→_j^(ext)· ∂r^→/∂q_i, obtain the equation of motion.

Q4. A mechanical system is described by the Lagrangian ⊥ = T - V with T = M/2[ω² + α²θ^· + 2αωθ^·sin(θ-ωt)], V = mg(sinωt-αcosθ), where α, ω, m and g are constants.

a) Find an equivalent Lagrangian, Lew.

b) Obtain the energy function, h.

c) Is h a constant of motion. Explain.

d) Is h identical to the total energy (E) of the system. Explain.

e) Is E a constant of motion. Explain.