Alternatives may include the use of commercial software like ANSYS but in that case the problem geometry and methodology for analysis – multiple meshes, careful examination of sensitivity of solutions to assumptions about material models and boundary conditions is expected.
The equation below is a simple model of heat transfer from a frame.
dT/dt - d/dx[k(dT/dx)] = hT
TA = TB = TC = TD =100
t = 0 T = 0
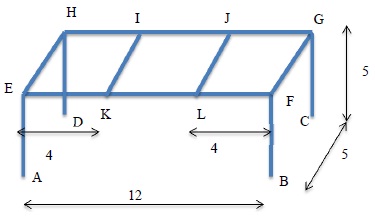
a) For k=0.5, h=2 develop an FEM code to solve for T on the space frame shown below in Figure. Use at least 6 elements per link. Use the generalized trapezoidal algorithm for time integration till t=10.
b) compute error indicator
E=.5√Σ[(∂T/∂n)]2 [(∂T/∂n)] |(∂T/∂n left-∂T/∂nright)|
for the case with linear elements and modify the mesh for the problem defined by adding new elements to locations where the error indicator is high, and, 2) by replacing them with quadratic or cubic elements. prepare a short report ~5 pages, analyzing your results and documenting the process by which you arrive at your final answer. [50% “Material Non Linearity” – Please replace the uniform k by k=0.5*(|T-100|)/100. Modify your code using the Newton-Rhapson or other procedure for dealing with material non-linearity.