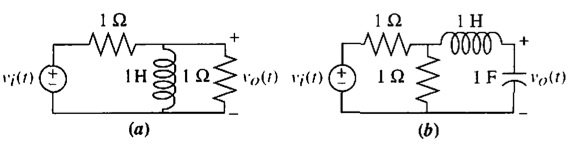
problem1) Find the transfer function, G(s) = V0(s)/Vi(s), for each network shown in figure given below:
problem2) Solve the following differential equation for 0
a) use the Runge Kutta method
b) use the ODE45 function
Plot the results
dy/dx = x2 * sin(x)
problem3) Three coupled street cars are moving at a speed of 32 km/hr down a 7 degree incline. Each car has a weight of 198 kN. The cars must stop within 50 m beyond the position where the breaks are fully applied so as to cause the wheels to lock. What is the maximum number of break failures that can be tolerated and still satisfy this specification? Assume that the weight is loaded equally among the wheels and that we have 24 brake systems, one for each wheel. Take μ=0.45.