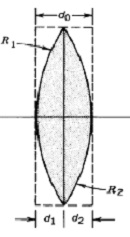
problem1. Derive that the complex amplitude of double convex lens shown below in the image with focal length
1/f = (n - 1)(1/R1 - 1/R2) . Hint: we derived a Plano convex lens in class.
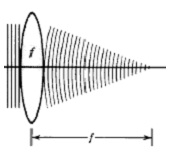
problem2. Show that when a plane wave is transmitted throughout a thin lens of focal length f in the direction parallel to the optical axis of the lens, it’s converted in a paraboloid wave (the Fresnel approximation of a spherical wave) centred about a point at a distance f from the lens.
problem3. A spherical wave is reflected towards a planar mirror sufficiently far from the wave origin so that the Fresnel approximation is satisfied. By regarding spherical wave locally as a plane wave with slowly varying direction, use the law of reflection of plane wave to determine the nature of the reflected wave.
problem4. Consider a thin transparent plate whose thickness d(x,y) is a square (instead of a sinusoidal) periodic function of x of period Λ=λ. Show that the angle θ between the diffracted waves is still given by θ = λ/Λ. If a plane wave is incident in a direction normal to grating, find out the amplitude of the dissimilar diffracted plane waves.
problem5. Show that a pulsed spherical wave has a complex wave function of the form U(r,t) = (1/r)a(t-r/c) where a(t) is an arbitrary function. An ultra short optical pulse has a complex wave function with a central frequency corresponding to a wavelength λ0 = 585nm and a Gaussian envelope of rms width σ 1 = 6fs. How many cycles are contained within the pulse width? If the pulse propagates in free space as a spherical wave initiated at the origin at t = 0, describe the spatial distribution of the intensity as a function of the radial distance at time t = 1ps.