problem: Consider the triangular laminar D for given b and h shown below:

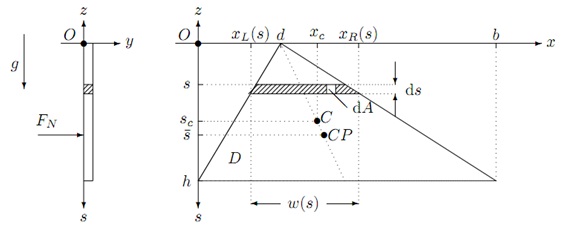
a) Find x_L(s) and x_R(s), the left and right ends of the elementary strip, of thickness ds, a distance s from the x-axis. Hence gives its width w(s) and the corresponding form for 1/2 [x_R(s) + x_L(s)].

b) Find, by direct integration, the area, A, of the lamina. Note we can regard the lamina as a rectangle from which two right-angled triangles are removed.

c) Find, by direct integration, the first moments of area, As_|O, Ax|_O, of the laminar. Hence find the position (x_c; s_c) of the centroid C relative to O.

d) Find, by direct integration, the second moments of area, Ass|_O ; Axs|_O of the laminar. Hence, using the parallel axis theorem, obtain Ass|C and Axs|C.

e) Suppose the triangular lamina is part of a vertical wall that separates fluid of density 1/2 from air at atmospheric pressure, p₀. Also gravity, of acceleration g, acts in the downward vertical s-direction with the horizontal x-axis (s = 0) lying a depth s₁ below the free surface. Find

i) The (resultant) hydrostatic force FN(s₁) acting on the lamina.
ii) The total moments of hydrostatic force Ms and Mx about the x and s-axes.
iii) The position (¹x; ¹ s), of the centre of pressure CP relative to the origin O.
iv) Show that the centroid and centre of pressure lie on the same line.

problem: In the system shown below, the force exerted by the free jet issuing from the sharp-edged circular nozzle and impinging on the small circular plate is just sufficient to keep the (isosceles) triangular door closed against the water pressure. The depth of the water in the tank is kept fixed by using top-up water. The mass of the arm, the circular plate and door are negligible. The door and the plate are each rigidly fixed to the arm, through their centroids.

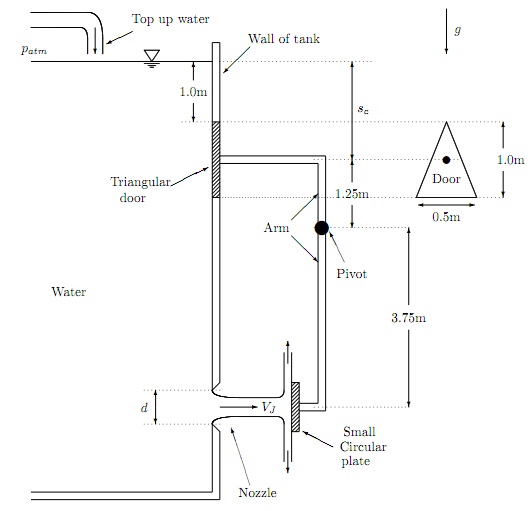
Neglect friction in both the water flow and the pivot, and take ρ = 1000 kg/m³ the density of water, and g = 9:81m/s² the acceleration due to gravity. Give full details of your assumptions, symbolic working and numerical calculations.

(a) Neglecting fluid motion (you can use results from Qu. 1) find (i) the horizontal hydrostatic force FN acting on the door, and (ii) the line of action of the hydrostatic force.

(b) Using Bernoulli's equation find the jet speed VJ.

(c) Draw a control volume focused only on the circular plate, and analyzes the linear momentum equation to find the horizontal hydrodynamic force FR acting on the plate in terms of nozzle diameter d.

(d) Finally, use moments to find the value of the diameter d.