problem1: Consider the noise cancellation system described below. The useful signal is a sinusoid s(n) = cos (wo n + Φ), wo = Π/12 where the phase Φ is a random variable uniformly distributed from 0 to 2 Π. The noise signals are given by:

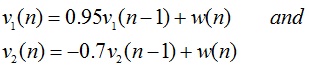
Where the sequence w(n) is WGN(0,1).

a) Design an optimum filter of order M and select a reasonable value M0 for M by plotting the MMSE as a function of M.

b) Design an LMS filter with M0 coefficients and choose the step size μ to achieve a 10% miss adjustment.

c) Plot the signals s(n), s(n)+v1(n), v2(n), the clean signal e₀(n) by using the optimum filter, and the clean signal elms(n) using the LMS filter and comment on the obtained results.

d) Re-solve the above noise cancellation problem by using the RLS and comment on the differences between RLS and LMS in terms of speed of convergence and excess error.

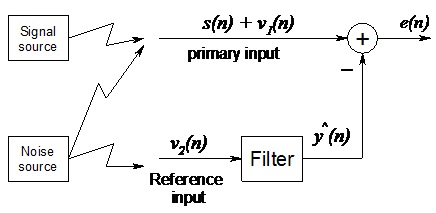
problem 2: Consider the process x(n) generated by using AR(1) model x(n) = - 0.729 x (n - 1) + w(n); where w(n) is WGN(0,1).
We want to design a linear predictor of x(n) using the Steepest Descent Algorithm (SDA). Let

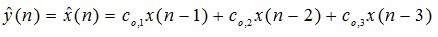
a) Find out the 3x3 autocorrelation matrix R of x(n) and compute its Eigen values.

{λi}³_i-1

b) Find out the 3x1 cross correlation vector d.

c) Choose the step size μ so that the resulting response is over damped. Now implement the SD

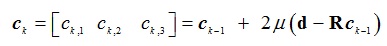
d) Repeat part (c) by choosing μ so that the response is under damped.