ASSIGNMENT - SOLID OF REVOLUTION

Finding Volume of Solid of Revolution

A. Find the volume of the solid formed by revolving the region bounded by the graph(s) of the equation(s) about the x-axis.

1. y = √(4 -x²)                        2. y = x²

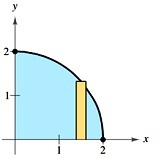
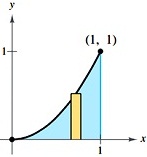
3. y = √x                                4. y = √(4 - x²)

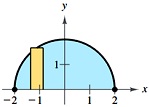
5. y = -x + 1, y = 0, x = 0        6. y = ex+1 + 1, y = x, x = 0

7. y = √x + 1, y = 0, x = 0, x = 9  8. y = ex, y = 0, x = 0, x = 1

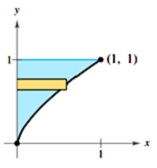
B. Find the volume of the solid formed by revolving the region bounded by the graphs of the equation(s) about the y-axis.

1. y = x², y = 4, 0 ≤ x ≤ 2          2. y = √(16 - x²), y = 0, 0 ≤ x ≤ 4

3. y = x^2/3                                      4. x = -y² + 4y

Problems

Direction: Apply Disk method or Washer Method to solve the following worded problems.

1. The line segment from (0,0) to (6,3) is revolved about the x-axis to form a cone. What is the volume of the cone?

2. Use the Disk method to verify the volume of a right circular come is 1/3Πr²h, where r is the radius of the base and h is the height.

3. Use the Disk Method to verify that the volume of a sphere of radius r is 4Πr³.

4. The upper half of the ellipse 9x² + 16y² = 114 is revolved about the x axis to form a prolate spheroid (shaped like a football). Find the volume of the spheroid.

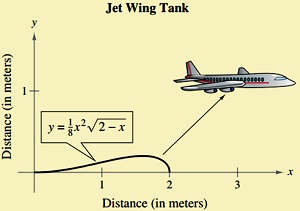
5. A tank on the wings of a jet airplane is modeled by revolving the region bounded by the graph of y = 1/8x²√(2- x) and the x-axis about the x- axis, where x and y are measured in meters (see figure). Find the volume of the tank.

6. A soup bowl can be modeled as a solid of revolution formed by revolving the graph of y = √(x/2 + 1), 0 ≤ x ≤ 4 about the x-axis. Use this model, where x and y are measured in inches, to find the volume of the soap bowl.

7. A pond is to be stocked with a species of fish. The food supply in 500 cubic feet of pond water can adequately support one fish. The pond is nearly circular, is 20 feet deep at its center, and has a radius of 200 feet. The bottom of the pond can be modeled by y = 20[(0.005x)² - 1].

a. How much water is in the pond?
b. How many fish can the pond support?

8. A regulation-size football can be modeled as a solid of revolution formed by revolving the graph of f(x) = -0.0944x² + 3.4 and -5.5 ≤ x ≤ 5.5 about the x-axis. Use this model to find the volume of a football. (In the model, x and y are measured in inches.)