Task: Analyze engineering problems and formulate mathematical model using first order differential equations

problem: A heated object is allowed to cool in a room temperature which has a constant temperature of T₀:

a) Analyze the cooling process
b) Formulate mathematical model for the cooling process.

problem: At time t = 0 water begins to leak from a tank of constant cross-sectional area A. The rate of outflow is proportional to h, the depth of water in the tank at time t. prepare the constant of proportion kA where k is constant.

a) Analyze the tank leaking process.
b) Formulate mathematical model for the leaking process.

prepare conclusions based on your formulated mathematical model for leaking process.

Task: Solve first order differential equations using analytical and numerical methods.

problem: Find the solution of the following equations:

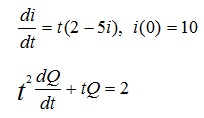
problem: Use the Euler method with the step size shown to advance four steps from the given initial condition with the given differential equation

dv/dt = 2t + V, V(0) = 1; h = 0.1

Task: Analyze engineering problems and formulate mathematical model using second order differential equations.

problem: For the simple model of a shock observer shown in figure below:

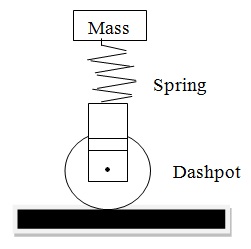
a) Analyze the model, vertical motion of the mass.
b) Formulate mathematical model of the model.

Task: Solve second order homogeneous and non- homogenous differential equations.

problem: Find the general solutions of the following equations:

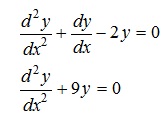
problem: Find the general solutions of the following equation which satisfy the given initial conditions.

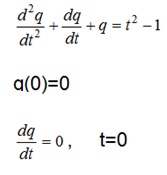
Task: Apply first and second order differential equations to the solution of engineering situations

problem: The velocity v of a rocket attempting to escape from the earth’s gravitational field is given by:

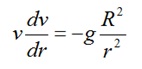
Where:

r is its distance from the centre of the earth and
R is the mean radius of the earth

Find a formula for V(r) and determine the minimum launch velocity V0 in order that the rocket escapes.