1) An incompressible, isothermal power law fluid is driven down a pipe of radius R and length L by an applied pressure gradient ∂P/∂z (a known negative value). Assume the flow is axisymmetric and gravitational effects are negligible, such that it is also possibly to assume ∂P/∂θ=0 (it is not necessary to show this, take it as an assumption). Furthermore, assume the flow is steady and fully developed in the downstream z-direction.

a) Solve for the velocity, shear stress distribution and the volumetric flow rate down the pipe. This does not require scaling.

b) Plot the velocity profile(s), varying n over the values 0.1, 0.2, 0.5, 1, 2, 5, 10. This is easiest if you normalize by the average velocity, which equals the volumetric flow rate divided by the cross-sectional area 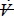/πR². Then plot , v_z /v_z, v_ave versus r/R

c) Though this solution does not require scaling, now show that the axisymmetric continuity equation specifies the relationship between L and R under which the fully developed assumption is valid.

2) Consider pressure driven flow of an incompressible, isothermal Bingham fluid between parallel plates of length L in the x-direction and gap 2h in the z-direction, where h << L. Assume the 2-D flow (plates are infinite in the y-direction) is steady, gravitational effects are negligible, v_y≡0, and ∂P/∂x is a known negative constant. Before you start, think about the best placement of your z-axis.

a) Assume the characteristic velocity in the x-direction is V_x and use scaling to estimate V_ZC.

b) Now use this result to estimate the components of the rate-of-deformation tensor. Then estimate γ^. = √II_γ^./2

c) Scale the appropriate component of the momentum equations and solve for v_x. What assumptions aboutRe_L and the geometry were necessary to neglect the inertia terms?

d) Now compute the “exact” value of γ^. = √II_γ^./2 based on the solution to the flow field. At what value of z is this exact value equal to the estimated value?

e) Plot the velocity profiles for several values of h_y /h.

3) Apply the material derivative D / Dt to the mass of a fluid particle m as follows:

Considering that the material derivative measures the rate of change while moving instantaneously with the fluid particle, evaluate Dm / Dt . Now, substitute m = ρ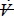 , and use the “alternative” form of compressible continuity in the notes, to relate
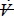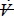1/ D/Dt
(the rate of volume increase of a particle, per unit volume) to the volumetric strain rate ε_ii (the dilatation or normal strain rate).

4) Simplify the general form of continuity for an incompressible, isothermal fluid. What does this tell us about the volumetric strain rate ε_ii (the dilatation or normal strain rate) in such a fluid? As we follow a fluid particle in this flow, what happens to its volume?