problem 1: (Hydrostatic pressure on curved 3-D surfaces)

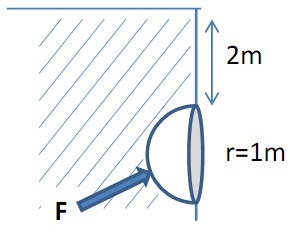
A shark tank in the aquarium has a hemispherical glass viewing “bubble” jutting into the water from the side wall. The radius of the bubble is 1m, starting 2m below the water surface. What is the horizontal and vertical resultant force of the water on the bubble?

problem 2: (Buoyancy of a floating body)

Ice has a density 91.7% of liquid water.  For an ice cube (1 cm per side):

a) what fraction of the volume floats above the water surface at standard pressure?
b) How does this fraction change if the air pressure increases by 2 psi?

problem 3: (Buoyancy of a submerged body; compressibility of air)

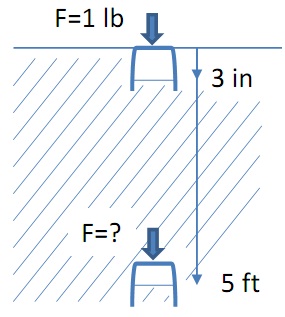
A grade 4 science student inverts a cup full of air into a water tank. If it takes 1 lb of force to hold the cup down 3 inches below the surface, how much force does it take to hold the cup down at a depth of 5 feet? Assume (1) the cup has negligible weight, (2) the temperature of the air is always the same as the surrounding water temperature.

problem 4: (Buoyancy; force & moment balance)

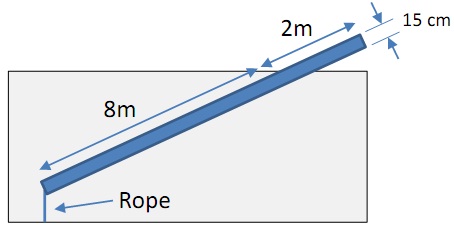
A partially submerged, homogeneous timber is 0.15m by 0.35m in cross-section. What is the specific weight of the timber and the tension in the rope holding one end down?

problem 5: (Rigid body acceleration)

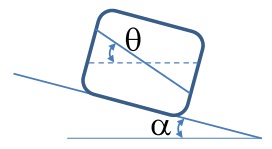
A tank of water accelerates down an icy frictionless ramp of angle α. What angle (θ) does the water make with the horizontal at equilibrium?

problem 6: (Rigid body rotation)

Derive the equation for the shape of the surface z_surf (r_surf) for a rigid-body rotation of water at angular speed ω (rad/sec).

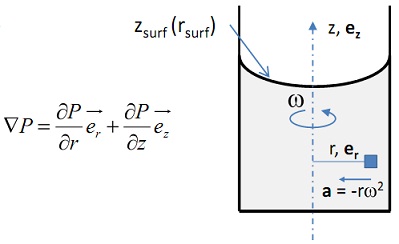
1) Start with pressure gradient in cylindrical coordinates:

2) prepare out force balance in r and z directions

3) Integrate using the method we did in class:

F = ma in r-direction gives:  P(r,z) = P(r) + f₁(z)
F = ma in z-direction gives:  P(r,z) = P(z) + f₂(r)

4) Solve for z(r) at surface, where P = P_atm = constant

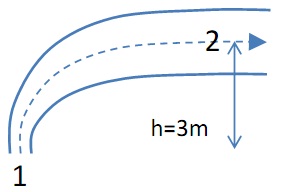
problem 7: (Bernoulli equation along a streamline)

Water flows from station (1) to (2) around an expanding corner pipe, 3m high.
The speed along the center streamline is 10 m/s at (1) and 5 m/s at (2).

a) What is the pressure difference between the stations (and which is higher)?

b) List all key assumptions inherent in your analysis.