problem 1: A cylindrical tank is used to store oil, as shown in Figure below. The weight of each tank W is 1800 kN. When subjected to an earthquake the horizontal inertial force, H, produced by the earthquake may be find outd as follows:
H = (W/g) a
Where g is the gravitational acceleration constant equal to 9.8 m/sec2 and a is the maximum horizontal acceleration of the earthquake ground motion.
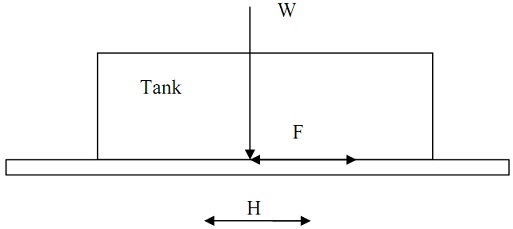
During an earthquake the frictional force, F, at the base of the tank keeps it from sliding. The coefficient of friction between the tank and the base support is normally distributed variable with mean 0.5 and coefficient of variation 0.1.
During an earthquake the maximum horizontal ground acceleration a is a random variable with the following probability density function:
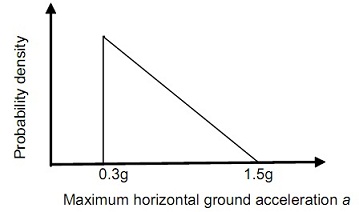
Estimate the probability that the tank will slide during an earthquake using Monte Carlo simulation.
Assume the coefficient of friction and horizontal ground acceleration are statistically independent.
Your program must use an adaptive replicate loop to ensure that probability estimates are within ± 0.001 of the true value with 99% confidence.
problem 2:
Consider the traffic roundabout shown in the Figure below:
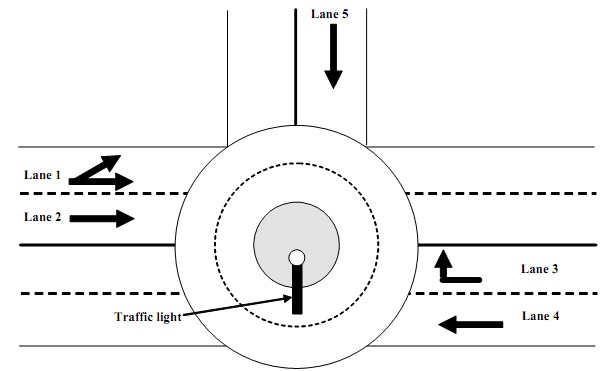
The traffic in lane 1 may proceed straight through the roundabout or turn left, while traffic in lane 2 can only proceed through the roundabout. Traffic in lane 3 can only turn right, while traffic in lane 4 can only proceed through the roundabout.
When operating, the traffic light displays either a red right arrow or a green right arrow. When a red arrow is displayed, traffic in lane 3 must stop at the entry to the roundabout, while traffic in lane 4 may enter the roundabout to pass through. When a green arrow is
displayed, traffic in lane 3 may turn right and traffic in lane 4 may proceed through the roundabout.
During the morning peak, the number of vehicles arriving at the intersection follows a Poisson process with the average number of arrivals being:
- 2000 cars/hr for lanes 1 and 2 combined;
- 700 cars/hr turning right from lane 3; and
- 0 cars/hr for lane 5.
The dynamics for traffic negotiating the roundabout are as follows:
1) Red arrow operating: One car from either lane 1 or 2 can enter the roundabout every second with probability 0.8. Traffic in lane 3 is stopped.
2) Green arrow operating: If there are no cars queuing in lane 3, one car from either lane 1 or 2 can enter the roundabout every second with probability 0.6.
If there are one or more cars queuing in lane 3, one car from lane 3 can enter the roundabout every second with probability 0.9. If the car in lane 3 does not enter the roundabout there is a 0.5 probability that a car in either lane 1 or lane 2 will exploit the gap and enter the roundabout.
prepare a Monte Carlo program to simulate the traffic queue at the roundabout. Run the simulation for 10,000,000 seconds under peak hour conditions using a one-second computational interval.
The roundabout is considered to be operating satisfactorily if the chance of a queue exceeding 20 cars in lanes 1 and 2 combined or in lane 3 is less than or equal to 10%.
Answer the following problems:
a) Show that if traffic lights are not used, the roundabout operates unsatisfactorily.
b) Using a trial-and-error approach determine the red and green arrow times that:
- Enable the roundabout to operate satisfactorily; and
- Balance the probabilities of queue lengths exceeding 20 in lanes 1 and 2 and lane 3.