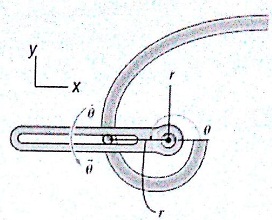
1. At a given instant the 6 kg block A is moving downward with a speed of 8 m/s. Determine (a) how far block A must descend to reach a speed of 19 m/s, how much time it takes to reach that speed and (c) the tension in the cable. Block B has a mass of 23 kg and the kinetic coefficient of friction between it and the horizontal plane is mu = 0.2

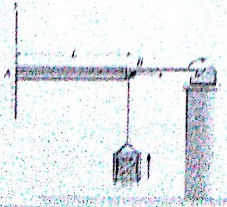
2. Determine (a) the minimum constant force required to lift the at-rest 250 lb block 7, 7 ft in 9 seconds and (b) the velocity of the cable at B with respect to block A at the end of the same time interval t = 9s.

3. The tanker with a total mass of 590,000 metric tons is traveling 3.1 m/s in still water when engines slop, Drag resistance force at any instant is F -7 v(3) , where v is in m/s and F is in MN or E6N or determine (a) the time needed to slow to 30% of the initial speed and (b) determine the distance traveled in this time.

4. A 420 kg crate is hoisted upward at a constant acceleration such that the fixed end moment of the beam to increases to 37500 N-m, If the beam length is 6.5 m, determine (a) the tension in the winch cable and (b) the magnitude of the acceleration of the lift.
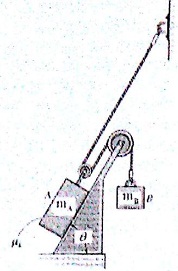
5. The surface shown is inclined to theta = 25 deg and has a coefficient of friction mu = 0.12. The weight of block A is 2500 lbs. Determine the acceleration of A and the tension in the cable for the following three cases: (a) the weight of B is (a) 160 lbs, (b) wtB = 1160 lbs and (c), wtB = 540 lbs.
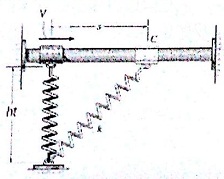
6. The 14 kg collar C slides freely on the smooth shaft. The spring is unstretched when s = 0 where it is given an initial velocity of 9 m/s. Determine (a) how far the mass slides before its velocity diminishes to zero if the spring constant k = 35 N/m and the dimension ht = 0.4 m. And (b) the normal force between the collar and smooth shaft.
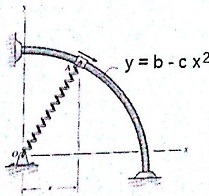
7. The 5 lb collar slides on the smooth rod having a parabolic path y = 18 - 0.7 * xA2. At the y = b -c X2 instant shown, the slider is at A where x = 3 ft, has a speed in the direction shown of 25 ft/s and is subjected to the force of a spring having an unstretched length and rate of 5ft and 2.3 lb/ft, respectively. Determine the (a) normal acceleration of the collar, (b) the normal force acting on the collar and (c) determine the collar peed that reduces the normal force to zero.
8. The particle shown is constrained to move along the slotted path defined by the horizontal hyperbolic spiral r*theta = 9/10 m. Determine (a) the Cartesian components of the particle's velocity at the instant the arm's angular position, velocity and acceleration are 2/8 pi radians, 8 rad/s and 5 rad/s/s, respectively. Also at this instant determine (b) the particle's acceleration in the polar (r, theta) system. Finally, also at this instant determine the magnitude of normal forces exerted by (c) the arm on the 2 kg particle and by (d) the spiral slot on the 2 kg particle.