problem 1: Describe any five parts:

a) Platinum resistance thermometer.
b) Adiabatic lapse rate.
c) Carnot theorem.
d) Plots of heat capacity (C_p) versus temperature (T) for the first order and the second order phase transitions.
e) Sedimentation.
f) Critical constants for dieterici’s equation.
g) Sackur-Tetrode equation.

problem 2:

a) What is a thermocouple? Describe its working principle. How is it used to measure the temperature? prepare down the range of temperature covered by:

i) A chromel-alumel thermocouple, and
ii) An iron-constantan thermocouple.

Describe merits and demerits of a thermocouple for temperature measurements.

b) Derive an expression of the work done by an ideal gas throughout an isothermal expansion of an ideal gas.

c) Two moles of a perfect gas occupy a volume of 0.060 m3 and exert a pressure of 4 × 10⁵ Nm⁻². It is compressed isobarically to 0.045 m³. Compute the work done by the gas.

problem 3:

a) Two kg of water is heated from 0°C to 100°C and transformed into steam reversibly. Compute the total increase in its entropy. Given, heat capacity of water = 4.2 × 10³ J kg⁻¹ K⁻¹ and latent heat of vaporization = 2.25 × 10⁶ J kg⁻¹.

b) For Carnot cycle, show that the amount of heat absorbed in a reversible cycle is proportional to the temperature of source. Compute the efficiency of a Carnot engine working between temperatures 560 K and 350 K.

c) prepare down the conditions for thermodynamic equilibrium of:

i) Thermally isolated – isochoric system,
ii) Thermally isolated – isobaric system,
iii) Thermally conducting – isochoric system, and
iv) Thermally conducting isobaric system.

problem 4:

a) Obtain Einstein’s formula for mean square displacement of a Brownian particle.

b) The coefficient of viscosity of helium at 300 K is 2 × 10⁻⁵ Nsm⁻². Compute the diameter of a helium molecule. Take average velocity of molecules as 1.26 × 10³ms⁻¹, Avogadro number as 6 × 10²³ mol⁻¹ and atomic weight of helium as 4.

c) Illustration the assumptions made by Vander Waals for real gases. How far does the real gas equation describe the observed results?

problem 5:

a) By using the expression for rotational partition function, get an expression for heat capacity of hydrogen. Depict its temperature variation.

b) The thermodynamic probability for a Fermi-Dirac system is given by:

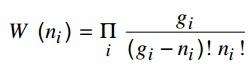
Get an expression for Fermi-Dirac distribution function. Plot the Fermi function f (ε) versus ε for a completely degenerate and a strongly degenerate system.