Task 1:
Introduction
In this task you are required to make use of use trigonometric functions, research and use the Monte Carlo, Trapezoidal and Lower and Upper Rectangle methods of integration to determine areas under curves and perform calculations on your results. Information on all these methods can be found in your text on page 236-248 (you must generate between 300 – 500 points for Monte Carlo method). All other research must be referenced.
Note: The scale on the horizontal axis 1radian = 1cm.
Your father has decided to give your mother an Anniversary gift of a gold and pearl pendant and asked you to design one for her.
Your father has the following instructions for the jeweller:
1. The pendant must be between 3 and 4 cm (inclusive) in length and 3 cm wide.
2. The gold should have a thickness of 4 mm.
3. The pearl must have a diameter of 1 cm.
You have experimented with various functions on your calculator and have decided on the following design:
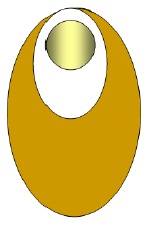
1. M2
Identify showing all working the trigonometric functions you have created that simulate the shape of the pendant. State any assumptions made.
2. K1
Using technology accurately graph the functions that match the designs and label the graphs.
3. M2
Use the Monte Carlo method and one of the other two methods to estimate the area of the gold. Fully justify your method with all graphs, formulae, spreadsheets shown and research done for these methods.
Be sure to state and justify any assumptions made.
4. K2
Demonstrate the calculus method to find the area of the gold on this pendant.
5. M3
Select the most accurate method to find the amount/area of gold required to make this pendant. Discuss the strengths and limitations of the model you have selected.
6. K2
Research the cost of gold and then find out the cost of gold to be used in the pendant. Show all calculations.