problem 1: Mixing problem
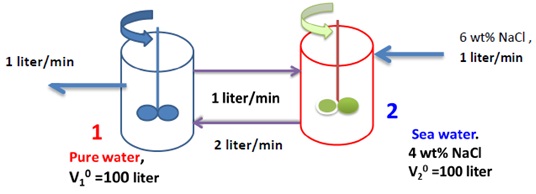
Two tanks initially contain 100 liter liquid each. Their initial concentration is listed in the Figure shown below. At time zero, the input and output valves are opened simultaneously with the similar flow rate of 1 liter/min. The feed into T2 is salty water with concentration of 6 wt% NaCl. In the meantime, the circulation begins between the two tanks with the rate of 1 liter/min and 2 liter/min, correspondingly (as shown in the below figure). You can suppose the tanks are well mixed. The density of liquid is constant at 1kg/liter.
Setup the mass balance equation for the salt amount in each tank and resolve the model by using:
a) Linear system method;
b) Laplace transform method.
c) Plot you results of the salt content (lb-salt) in each tank as a function of time (minutes).
problem 2: Solve the Laplace transforms:
y” + 3y’ - 4y = 6 e2t-2, y(1) = 4, y’(1) =5.
problem 3: Find out the Laplace transform:
Sin(t) * Cos(t)
(Use the integration method, differential methods and so on. Please don’t use the simple way of converting to sin(2t)).
problem 4: Solve the ODEs by using linear system and also Laplace method:
y” + 5y’ +4y = 2e-2t, y(0) = 0, y’(0) = 0