Answer all problems showing all working:
problem1) Everybody’s blood pressure varies over the course of the day. In a certain individual the resting diastolic blood pressure at time t is given by B(t) = 80 + 7 sin (πt/12), where t is measured in hours since midnight and B(t) in mmHg (mm of mercury). Find this person’s diastolic blood pressure at
a) 6:30 AM
b) 10:30 AM
c) Noon
d) 8:00 PM

problem 2) After the switch is closed in an LCR electrical circuit (one with a resister, inductor and capacitor), the current t seconds later is I(t) = 0.8e-3tsin10t. Find the current at the following times
a) t = 0.05s
b) t = 0.1s
c) t = 0.25s
d) t = 0.5s

problem3) Variable stars are ones whose brightness varies periodically. One of the most visible is R Leonis; its brightness is modelled by the function

b(t) = 7.9-2.1 cos(Π/156t)

where t is measured in days.
a) Find the period
b) Find the maximum and minimum brightness values
c) Graph its function

problem4) The frequency of oscillation of an object suspended on a spring depends on the stiffness k of the spring (called the spring constant) and the mass m of the object. If the spring is compressed a distance a and then allowed to oscillate, its displacement from its starting point is given by

f(t) = a cos√(K/mt)

a) A mass of 10g is suspended from a spring with stiffness k = 3. If the spring is compressed a distance 5 cm and then released, find the equation that describes the oscillation of the spring.
b) Find a general formula for its frequency of oscillation (in terms of k and m).
c) How is the frequency affected if the mass is increased? Is the oscillation faster or slower?
d) How is the frequency affected if a stiffer spring is used (larger k)? Is the oscillation faster or slower?

problem5) Memphis, Tennessee, and New Orleans, Louisiana, lie approximately on the same meridian. Memphis has latitude 35°N and New Orleans has latitude 30°N. Find the distance between these two cities. (The radius of the earth is approximately 3960 miles).

problem 6) An irrigation system uses a straight 30m sprinkler pipe which is capped at one end and arranged so that all water is released directly downwards and pivots around a central point. Due to an obstacle the pipe is allowed to pivot through 280° only. Find the area irrigated by this system.

problem7) From the top of a 200 m lighthouse, the angle of depression to a ship in the ocean is 23°. How far is the ship form the base of the lighthouse?

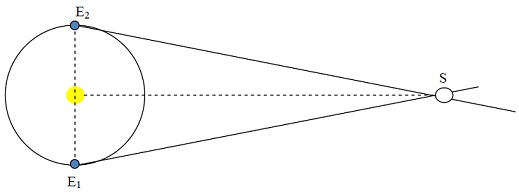
problem8) To find the distance to nearby stars, the method of parallax is used. The idea is to find a triangle with the star at one vertex and with a base as large as possible. To do this, the star is observed at two different times exactly 6 months apart, and its apparent change in position is recorded. From these two observations,1SE₂can be find outd. (The times are chosen so that 1SE₂ is as large as possible, which guarantees that 1OSis 90°.) Alpha Centauri, the star nearest the earth, the measured angle 1SE₂ has been found to be 0.000422°. Estimate the distance to this star. (Use 9.3 x 10⁷ miles as the distance from the earth to the sun)

problem9) The time in seconds that it takes for a sled to slide down a hillside inclined at and angle θ is

t= √(d/16 sin θ)
where d is the length of the slope in metres. Find the time it takes to slide down a 2 km slope inclined at 30°.
problem10) A 50-foot pole casts a shadow on the ground.
a) Express the angle of elevation θ of the sun as a function of the length s of the shadow. (Hint you may wish to draw this first)
b) Find the angle θ of elevation of the sun when the shadow is 20 feet long.

problem11) A pilot is flying over a straight length of road. He determines the angles of depression of two mileposts, 5 miles apart, to be 32° and 48°.
a) Find the distance of the plane from one of the mileposts.
b) Find the elevation of the plane. (hint the angle of depression is between the flight line of the plane and the milepost)

problem12) Two boats leave the same port at the same time. One travels at a constant speed of 30 km/hr at a bearing of 50° and the other on a bearing of 110° at a constant speed of 26 km/hr. How far apart are the two boats after 2 hours?
problem13) A 125-foot tower is located on the side of a mountain that is inclined at 32° to the horizontal. A guy wire is to be fitted to the top of the tower and anchored at a point 55 feet downhill from the base of the tower. Find the shortest length of wire needed.