problem: Suppose a company has fixed costs of $57,600 and variable costs of (1/3) x + 333 dollars per unit, where x is the total number of units produced. Suppose further that the selling price of its product is 2165 – (2/3) x dollars per unit.
(a) Find the break-even points. (Enter your answers as a comma-separated list.) x =?
(b) Find the maximum revenue. (Round your answer to the nearest cent) $ = ?
(c) Form the profit function, P(x), from the cost and revenue functions. P(x) =?
(d) Find maximum profit. (Round your answer to the nearest cent) $ = ?
(e) What price will maximize the profit? (Round your answer to the nearest cent) $ = ?
problem: The following table shows worldwide sales of cell phones by a certain company and their average wholesale prices in the first quarters of 2009 and 2010.
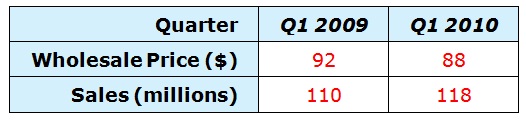
(a) Use the data to obtain a linear demand function for the company's cell phones. (Let p be the price, and let q be the demand).
q(p) = ?
Use your demand equation to predict sales if the company lowered the price further to $85.
(b) Fill in the blank.
For every $1 increase in price, sales of cell phones decrease by ……….. million units.
problem: The RideEm Bicycles factory can produce 140 bicycles in a day at a total cost of $10,400 and it can produce 160 bicycles in a day at a total cost of $11,100. What are the company's daily fixed costs? $
What is the marginal cost per bicycle?
problem: In November 2010, a financial service company was offering only 0.4% interest on its online savings accounts, with interest reinvested monthly. In November of which year will an investment of $5,000 made in November of 2010 first exceed $5,200?
problem: A car that was being pursued by the police was at Jones Beach at exactly 9:12 pm (t = 9.2) and passed Oak Beach (15 miles from Jones Beach) at exactly 9:24 pm, where it was overtaken by the police.
(a) How fast was the car traveling?
(b) How far was the car from Jones Beach at time t?
problem: You operate a gaming Web site, www.mudbeast.net, where users must pay a small fee to log on. When you charged $4 the demand was 580 log-ons per month. When you lowered the price to $3.50, the demand increased to 870 log-ons per month.
(a) Construct a linear demand function for your Web site and hence obtain the monthly revenue R as a function of the log-on fee x.
(b) Your Internet provider charges you a monthly fee of $50 to maintain your site. Express your monthly profit P as a function of the log-on fee x.
Determine the log-on fee you should charge to obtain the largest possible monthly profit.
What is the largest possible monthly profit?
problem: During the period 1990–2001, U.S. imports of pasta increased from 270 million pounds in 1990 (t = 0) by an average of 40 million pounds/year.
(a) Use these data to express q, the annual U.S. imports of pasta (in millions of pounds), as a linear function of t, the number of years since 1990.
(b) Use your model to estimate U.S. pasta imports in 2006, assuming the import trend continued.
problem: Gymnast Clothing manufactures expensive hockey jerseys for sale to college bookstores in runs of up to 150. Its cost (in dollars) for a run of x hockey jerseys is:
C(x) = 1500 + 10x + 0.2x2 (0 ≤ x ≤ 150)
Gymnast Clothing sells the jerseys at $90 each. Find the revenue function.
Find the profit function.
How many should Gymnast Clothing manufacture to make a profit?
problem: A function is given. Determine the average rate of change of the function between the given values of the variable.
f(x) = 7 − x2; x = 2, x = 2 + h
problem: A piano manufacturer has a daily fixed cost of $1,600 and a marginal cost of $1,800 per piano. Find the cost C(x) of manufacturing x pianos in one day.
Use your function to answer the following problems.
(a) On a given day, what is the cost of manufacturing 3 pianos?
(b) What is the cost of manufacturing the 3rd piano that day?
(c) What is the cost of manufacturing the 11th piano that day?
(d) What is the variable cost?
What is the fixed cost?
What is the marginal cost?