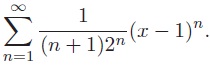problem 1

This problem tests your ability to describe symmetries geometrically and to represent them as permutations in cycle form. It also tests your understanding of conjugacy classes and their relationship to normal subgroups.
The figure below shows a prism with three congruent square faces and an equilateral triangle at the base and the top. The locations of the vertices of the prism have been numbered so that we may represent the elements of the group G of all symmetries of the prism as permutations of the set {1, 2, 3, 4, 5, 6}.

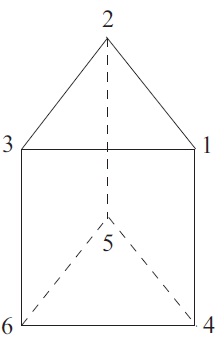
(a) Describe geometrically the symmetries of the prism represented in cycle form by (1 6)(2 5)(3 4) and (2 3)(5 6).
(b) prepare down all the symmetries of the prism in cycle form as permutations of {1, 2, 3, 4, 5, 6}, and describe each symmetry geometrically.
(c) prepare down the conjugacy classes of G.
(d) Determine a subgroup of G of order 2, a subgroup of order 4, and a subgroup of order 6. In each case, state whether or not your choice of subgroup is normal, justifying your answer.

problem 2

This problem tests your understanding of matrix groups and conjugate subgroups.

This problem concerns the group of matrices

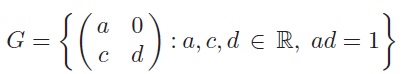
under matrix multiplication, and its subgroups

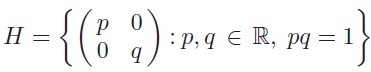
and

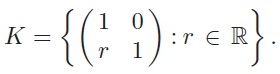
(You are NOT asked to prove that any of G, H and K are groups.)
(a) Use the strategies in Frame 10 of Section 5.2 of Unit GTB1 to show that one of H and K is a normal subgroup of G, but the other is not.
(b) For the subgroup which is not normal, determine two other subgroups of G to which it is conjugate.

problem 3

This problem tests your understanding of homomorphisms, kernels, images and quotient groups. In this problem C∗ is the group of non-zero complex numbers under multiplication, and C is the group of all complex numbers under addition.

(a) Determine whether or not each of the following functions is a homomorphism.

(i) φ1 : C → C
      z → z + 3i
(ii) φ2 : C → C
      z → z + 3iz
(iii) φ3 : C∗ → C∗
      z → 2z²
(iv) φ4 : C∗ −→ C∗
      z →z/z

(b) For each homomorphism φ in part (a), determine Ker(φ) and Im(φ), and identify the quotient group G/ Ker(φ) up to isomorphism, where G is the group that is the domain of the homomorphism. (That is, specify a group from the module that is isomorphic to G/ Ker(φ).)

problem 4

This problem tests your understanding of group actions, orbits and stabilisers.
This problem concerns the subgroup

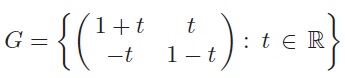
of the group M of 2 × 2 invertible matrices under matrix multiplication.
(You are NOT asked to prove that G is a subgroup of M.)
(a) Show that the following equation defines a group action of G on the plane R²:

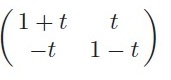∧ (x, y) = ((1 + t)x + ty, −tx + (1 − t)y).
The remainder of this problem concerns the group action given in part (a).

(b) Determine the orbits of:

(i) (1, 0),
(ii) (1, 1),
(iii) (1,−1).

(c) Give a geometric description of ALL the orbits of the action.

(d) Determine the stabilisers of:

(i) (1, 1),
(ii) (1,−1).

problem 5

This problem tests your understanding of the Counting Theorem. A large square is to be made from eight congruent triangular tiles, fitted together as shown in the diagram below. Each triangular tile can be black or white.

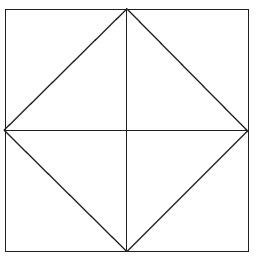
Use the Counting Theorem to determine how many different such squares can be made, if two squares are regarded as the same when a rotation or reflection takes one to the other.

problem 1

This problem tests your understanding of limits, the ε–δ definition of continuity and uniform continuity, and your ability to give careful proofs and to apply esults involving these concepts.
(a) In this part of the problem you may assume any results that are proved in Unit AB1, but you should refer to any result that you use. Prove each of the following statements.

(i) lim_x→1 (2x³ − 5x² + 2x + 1)/(x² − 4x + 3)= 1
(ii) lim_x→0 (sin x)/ (e^{sin x} − 1)= 1
(iii) lim_x→∞(4x⁴ − log_e x)/(2e^x + 3x²)= 0

(b) Prove that the following function does not tend to a limit as x tends to zero.

f(x) = (3x³ − 4|x|)/ 2x
(c) Use the ε–δ definition of continuity to prove that the function

f(x) = 2x² − 3x is continuous at 2.
(d) Prove that the function
f(x) =(x − 2)/(x + 1)
is uniformly continuous on the interval [1, 3], stating any results from the module which you use.

problem 2

This problem tests your ability to determine whether a function is differentiable at a given point, and to apply theorems relating to differentiability.
(a)

(i) Prove from the definition of differentiability that the function

f(x) =(x − 2)/(2x + 1)
is differentiable at 2, and find f'(2).
(ii) Sketch the graph of the function
f(x) = (x2 − x, x ≤ 2, 2x − 2, x> 2.)

Determine whether or not the function f is differentiable at 2.

(b) Use the Mean Value Theorem to show that if
f(x) = sinx/x
then there is a point c in (π/4,π/2) such that f'(c) = − 8(√2 − 1)/π²
(c)

(i) Prove the following inequality:
x^6/7 ≤ 6/7x + 1/7 , for x ∈ [0, 1].

(ii) State whether the following inequality is true or false, giving a brief reason for your answer:
x^7/5 ≤ 5/7x + 1/7 , for x ∈ [0, 1].
(d) Prove that the following limit exists, and evaluate it.
lim_x→1[1 − sin{(π/2)x}] /( x⁴ − 2x² + 1)

problem 3

This problem tests your understanding of the ideas behind Riemann integration, your ability to evaluate integrals using various techniques, and your ability to apply results relating to integration.
(a) Let f be the function

                      { 3, x= −2,
      f(x) =       −x, −2 < x ≤ 0,
                     2x + 1, 0 < x < 2,
                      3, x= 2.}

Sketch the graph of f, and evaluate L(f, P) and U(f, P) for each of the following partitions P of [−2, 2].

(i) P = {[−2, 0], [0, 2]}
(ii) P = {[−2,−3/2 ], [−3/2 , 0], [0, 1], [1, 2]}
(b) Let

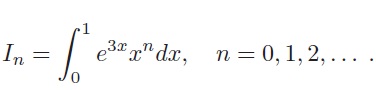
(i) Evaluate I₀.
(ii) Show that a reduction formula for In is
In = 1/3e³ − 13nI_n−1, for n ≥ 1.
(iii) Deduce the values of I₁ and I₂.
(c)

(i) Show that

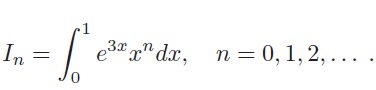
(ii) Hence determine whether the series

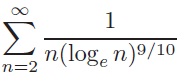
convergence or divergence

(d) Use Stirling’s Formula to determine a number λ such that
(6n)!/((2n)!)3 ∼ λ(3⁶ⁿ/n)as n→∞.

problem 4

This problem tests your ability to determine a Taylor polynomial and a remainder estimate, to determine the interval of convergence for a power series, and to apply the General Binomial Theorem.
(a)

(i) find out the Taylor polynomial T₂(x) at −1 for the function

f(x) =(1/1 − 2x)
.
(ii) Show that T₂(x) approximates f(x) with an error of less than 1/80 on the interval [−1.5,−1]. [9]
(b) Determine the interval of convergence of the power series

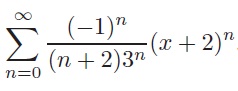
(c)

(i) Use the General Binomial Theorem to determine the first four terms of the Taylor series at 0 for the function
f(x) = (1 + 5x)^−1/5.
State the radius of convergence of this power series.

(ii) Using the Taylor Series in part (c)(i) with a suitable value of x, show that
2^1/5 = 1+1/((1!) × 10)+(1 × 6)/((2!) × 100)+(1 × 6 × 11)/(3!) × 1000+.....

problem 1

Consider the following sets:
A = {(x, y) ∈ R² : (x − 2)² + (y + 1)² < 9},
B = {(x, y) ∈ R² : y − 2x < 2}.
Show that A is a proper subset of B.

problem 2

The set {1, 2, 4, 8, 16, 32, 64, 128} forms a group G under multiplication modulo 255. (You are NOT asked to prove this statement.)
(a) Show that G is cyclic.
(b) Find all the subgroups of G.
(c) Find an isomorphism φ that maps (G,×₂₅₅) to (Z_8,+₈).

problem 3
The group table for a group G is shown below

(a) Show that H = {e, a} is a subgroup of G.
(b) prepare down the distinct left cosets of H in G.
(c) Show that H is a normal subgroup of G.
(d) Construct the group table for the quotient group G/H and prepare
down a group from the module to which G/H is isomorphic.

problem 4

A regular hexagon OPQRST has its vertices at O (the origin) and points P, Q, R, S and T with position vectors p, q, r, s and t, respectively. The point U with position vector u is the midpoint of the line segment OP, and SU meets OR at the point V

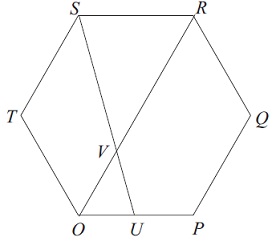
(a) Show that the position vector r = 2(p + t) and prepare down the position vectors u and s, in terms of p and t.
(b) Show that each point on the line SU can be represented by a vector x of the form
x = (1/2 + 1/2λ)p + 2λt, where λ ∈ R.
(c) Find the value of λ, in the above formula, for which x is a multiple of r.
(d) Hence find the position vector v of the point V , and prepare down the ratio UV : V S.

problem 5

Let t be the linear transformation
t : R³ → R³
(x, y, z) → (x + 3y + z,−x + y + z, x+ 5y + 2z).
(a) Find Ker(t) and state its dimension.
(b) Find a basis for Im(t).
(c) Describe Im(t) geometrically and obtain an equation for it.
(d) Determine how many solutions the following system of linear equations has:
                                x + 3y + z = 1,
                               −x + y + z = 1,
                                x + 5y + 2z = 1.

problem 6

Determine whether each of the following sequences {a_n} is convergent, stating the limit of the sequence if it exists. You should name any result or rule you use.
(a) an = (6n² − 2n)/(3n² + 3n − 7), n = 1, 2, . . .
(b) an = (5n² + (−3)ⁿ + n)/(3ⁿ − 2 + 2ⁿ) , n = 1, 2, . . .
(c) an = (2n⁸ + n! + 2ⁿ)/(3ⁿ + 4), n = 1, 2, . . .

problem 7

Let f be the function defined by

f(x) =    {sin x, x < 0,
            2x, 0 ≤ x < 1,
            cos(πx), 1 ≤ x.}

(a) Sketch the graph of f.
(b) Prove that f is continuous at 0.
(c) Prove that f is discontinuous at 1.

problem 8

This problem concerns the symmetry group G of the regular hexagon, shown below.

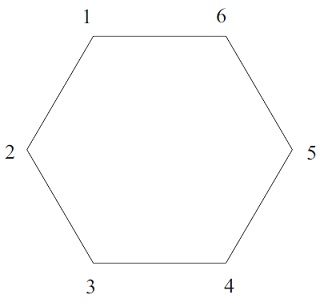
Let g ∈ G be the anticlockwise rotation of the hexagon through an angle of 2π/3 about its centre, and let h ∈ G be the reflection of the hexagon in the line through the midpoints of sides 12 and 4 5.
(a) prepare g, g² and h in cycle form, using the numbering of the locations of the vertices as shown above.
(b) Express the conjugate ghg⁻¹ of h by g in cycle form, and describe ghg⁻¹ geometrically.
(c) Are the symmetries (1 6)(2 5)(3 4) and (1 4)(2 5)(3 6) conjugate in G? Justify your answer.
(d) Are the symmetries (1 6)(2 5)(3 4) and (1 4)(2 5)(3 6) conjugate in S₆? Justify your answer.
(e) prepare down the conjugacy class of G that contains (2 6)(3 5).

problem 9

Let G be the group of matrices

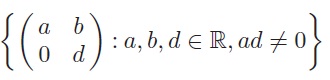
under matrix multiplication, and let f : G → G be the function defined by

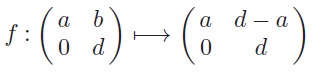
(a) Show that f is a group homomorphism.
(b) Determine the kernel of f.
(c) Find a group of matrices that is isomorphic to the quotient group G/ Ker(f).

problem 10
Show that the following limit exists and determine its value.
lim_x→1 (x + cos(πx))/(3x⁵ − 5x³ + 2x)

problem 11

Prove that

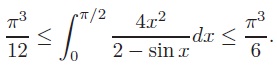
problem 12

Determine the interval of convergence of the power series