Problem must demonstrate how graphing can be accomplished using what you learned in calculus. Draw graphs. Annotate all features of the graphs including maximums and minimums, changes in concavity, intervals of increasing and decreasing, and asymptotes. Show how the various features of the graph were find outd using methods from calculus. Well-documented graphs with additional features included that demonstrate the concepts will receive extra Credit. 

1. Graph the following

a. y = ln(sin(x) + 1)

b. y = ln(sin(x) +2)

c. x y = xe^x

d. x² = y e^-x

2. Find the derivatives of the following

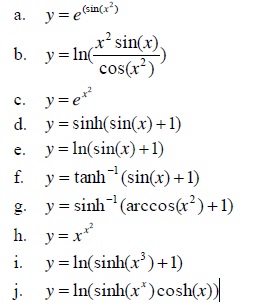
3. Evaluate the following

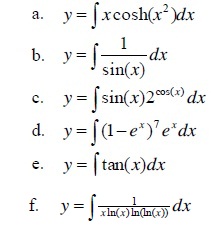
4. Suppose that the rate of inflation over the next 60 years will be 3%, the rate of your Income growth will be 4% over the next 30 years, and the rate of your investments will also be 4%. Assume continuous growth of salary, savings, etc.

a. If your first job pays $40K/year, what will be your annual salary after 30 years?

b. How much will you make in total over 30 years?

c. Suppose that when you retire in 30 years, you want to have half your salary (at That time) available for 30 more years. How many total investments should you have at the time you retire?

d. How much should you save every year on order to have the proper amount Invested when you retire?

5. Redo #4 assuming a pay raise once a year and deposits and withdraws accrue yearly, Monthly, and daily rather than continuously.