problem)Atmospheric carbon dioxide is thought to be responsible for global warming.
The table below contains data about the amount of Atmospheric CO2 (in ppm) over the last fifty years.
Year CO2
1959 315.98
1960 316.91
1965 320.04
1968 323.04
1971 326.32
1975 331.08
1980 338.7
1982 341.4
1984 344.4
1986 347.2
1988 351.5
1990 354.2
1992 356.4
1994 358.9
1996 362.6
1998 366.6
2000 369.4
2002 372.9
2007 383.71
2008 385.54
2009 387.35
(a) Construct a scatter plot for this data. (Either by hand or using Excel)
(b) Comment on the shape.
(c) Find a line of best fit. If doing this by hand, you will need to find the line of best fit by eye and then find the equation. If using excel, use a formula(s) to find the line of best fit.
(d) Using the equation, what was/is the atmospheric CO2 in 2005, 1920, 2020? Comment on the accuracy of your answers.
(e) In your conclusion, comment on the accuracy of modeling this as a straight line given your graph. Consider the accuracy to determine past and present values for CO2.
Data sourced from http://co2now.org/index.php?option=com_content&task=view&id=22&Itemid=1
problem)Forensic Science – Bone Lengths
Forensic Scientists can estimate the height of deceased people from the length of a few key bones.
Heights can be determined from the length of the humerus, (the bone that extends from the elbow to the shoulder) using the equations:
For males: H= 3.08h + 70.45, For females H=3.36h + 57.97
Where H is the height of the deceased and h is the length of the humerus in cm.
Heights can also be estimated from the length of the tibia, (the larger bone that extends from just below the kneecap to the ankle) using the equations:
For males: H=2.42t + 81.93, for females H=2.9t + 61.53
Where H is the height of the deceased and t is the length of the tibia in cm.
Heights can also be estimated from the length of the ulna, (the larger bone that extends from the elbow to the hand) using the equations:
For males: H=3.7u + 70.45, for females H=4.27u + 57.76
Where H is the height of the deceased and u is the length of the ulna in cm.
What is the height of the person and are they male or female?
Complete the following:
(a) A tibia of length 32 cm is found in a burial site, find the person’s height? (the sex is unknown)
(b)A collection of bones is found where the humerus = 34cm, tibia = 38.5cm and ulna = 28.3cm. Was this person a male or female
Based on your height, what will the length of your humerus, tibia and ulna be?
problem) Tyre Life
Data about tyre wear was collected. The number of kilometres from Brand A tyres is given below:
The number of kilometres from Brand A tyres is:
35000 38000 38000 42000 45000
45000 49000 50000 50000 52000
53000 58000 62000 62000 63000
66000 67000 70000 71000 74000
76000 81000 81000 86000 94000
The number of kilometres from Brand B tyres is:
46000 49000 55000 56000 58000
64000 64000 64000 67000 68000
68000 69000 69000 72000 72000
74000 76000 78000 79000 79000
82000 86000 87000 94000 97000
Which tyre gives the longest life?
(a) Draw a side by side box and whisker plot to determine the answer. (Hint: arrange the data in a back to back stem and leaf plot first)
problem 3 Male and Female Athletes
The table below contains times for males and females times for 100m running races at Olympic Games.
Year Years since 1928 Men’s 100m time (sec) Women’s 100m time (sec)
1928 0 10.8 12.2
1932 4 10.3 11.9
1936 8 10.3 11.5
1948 20 10.3 11.9
1952 24 10.4 11.5
1960 32 10.2 11.0
1968 40 9.95 11.08
1976 48 10.06 1.08
1980 52 10.25 11.06
1992 64 9.96 10.82
1996 68 9.84 10.94
2000 72 9.87 10.75
2004 76 9.85 10.93
2008 80 9.69 10.78
Construct a graph for this data. (Either by hand or using Excel)
Determine the equation for the line of best fit by both calculation and using excel. Compare the two answers.
Will female athletes ever catch up to male athletes? When might this happen?
problem 4 Household Water Use
1. This is a roof plan (from above) of a house.
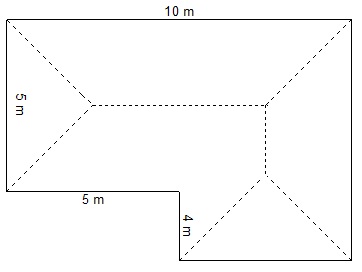
(a)During a recent rainy day, 72 mm of rain was recorded. find out how many litres of water will be collected from the roof and stored in the water tank. Remember 1cm3 = 1mL or 1m3 = 1kL(1000L)
The volume V of water in the tank, initially full, remaining after (d) days is given by the equation:
V=10 000-235 d
(b) How much is left from a full tank after 30 days of no rain?
(c) From the equation, determine how many litres of water the tank holds when full.
(d) From the equation, determine how many litres of water the householders use per day
(e) When will the volume of the tank be reduced to 2500 litres?
problem 5 Break-even analysis
A tourist coach company offers a daily (week days) tour from Bryon Bay to Lismore and return. People taking the tour are supplied lunch
The company puts a weekly advertisement in the local paper costing $120.
Pc = $120.00
Each passenger is charged $45 (including lunch) for the return journey.
Ep=$45.00
The fuel cost and other running costs total $45 per trip.
F=$45.00
The driver’s wage is $120 per trip.
Dw=$120.00
Lunch cost is $14 per person
L=$14.00
Outlay = Pc=$120c a week, F=$45, Dw=$120= $299.00 Each trip costs= $285
Variable =, Lunch=$14
Income = Per passage Ep=$45 ($30)
P=$120+$120+$45=$285
If clients pay $45 and this cost is called $31 then this removes the variable in the equation of the $14 for lunch.
10 clients per trip to make a profit
The company would like to make a profit on a weekly basis even though some individual trips might operate at a loss.
(a) From the information given, plot the graphs of revenue and cost and find the number of passengers required per week to break even.
(b) Ideally the company would like to make $1000 profit per week, find out the number of passengers required to make this happen.
(c) What is the maximum profit possible if the bus can hold a maximum of 20 passengers per trip?