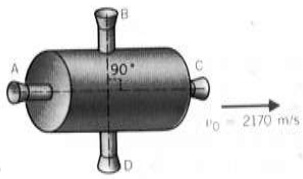
problem 1: The spacecraft in the figure shown below has a mass of 4160 kg and is traveling at speed of 2170m/s in the direction shown. The ship has 4 engines A, B, C and D, each of which can give 68,000 N of force in the direction they point. What engines must be fired and for how long, to change the velocity of the spacecraft so that the velocity has twice the original magnitude and the ship is traveling in a direction 90° clockwise relative to the original direction.

(Note: you don’t have to turn the ship it travels in its original orientation.)

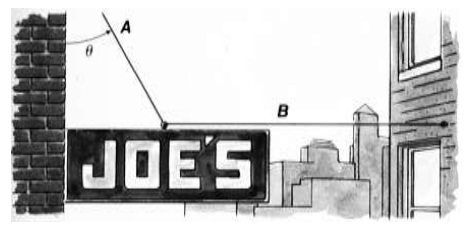
problem 2: Joe wishes to hang a sign weighing 750N so that cable A joined to the store makes a 30° angle as shown by θ in the figure. Cable B is attached to an adjoining building. Compute the tension require in cable B.

problem 3: Sarah pulls her 18.0 kg suitcase at a constant speed by pulling on a handle that makes an angle θ with the horizontal. The frictional force on the suitcase is 27.0 N and Sarah applies a 43.0 N force on the handle.

a) What angle does the handle make with the horizontal?
b) What is the normal force applied on the suitcase?

problem 4: You place a box weighing 215 N on an inclined plane which makes a 35.0° angle with the horizontal.

a) find out the component of gravitational force acting down the plane. (Friction is not a factor).
b) Determine the acceleration of the box?

problem 5: You slide a 325N trunk up a 20.0° inclined plane with a constant velocity by applying a force of 211 N parallel to the plane.

a) What is the component of the trunks weight parallel to the plane?
b) Find out the sum of your applied force, friction and the parallel component of the trunks weight?  Why?
c) Find out the size and direction of the frictional force?