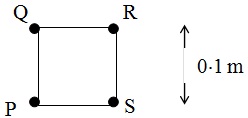
problem 1: Four point charges P, Q, R and S each of +4.0 nC are placed at each of the corners of a square of side 0.10 m.

a) Find out the electrostatic force, magnitude and direction, on charge P.
b) What is the electrostatic force on a -1.0 nC charge positioned at the centre of the square? You should justify your answer.

problem 2: A proton and an electron encompass an average separation of 2.0 × 10^-10 m. Compute the ratio of the electrostatic force FE to the gravitational force FG acting on the particles.

Use G = 6.67 × 10^-11 N m² kg^-2.

problem 3: Assume that the Earth (mass 6.0 × 10²⁴ kg) has an excess of positive charge and the Moon (mass 7.3 × 10²² kg) has an equivalent excess of positive charge. Compute the size of the charge needed so that the electrostatic force between them balances the gravitational force among them.

problem 4: The diagram below exhibits three charges fixed in the positions shown below.

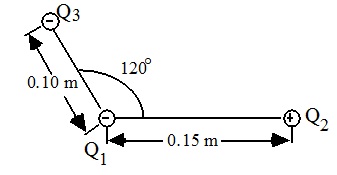
Q₁ = – 1.0 × 10^–6 C, Q₂ = + 3.0 × 10^–6 C and Q₃ = –2.0 × 10^–6 C.

Compute the resultant force on charge Q1. (Keep in mind that this resultant force will have a direction and also magnitude).

problem 5: In an experiment to show Coulomb’s law, an insulated, light, charged sphere is brought close to the other similarly charged sphere that is suspended at the end of a thread of length 0.80 m. The mass of the suspended sphere is 0.50 g.

It is found that the suspended sphere is displaced to the left by a distance of 16 mm as illustrated below.

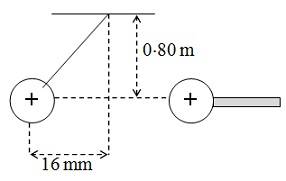
a) Make a sketch exhibiting all of the forces acting on the suspended sphere.

b) Compute the electrostatic force acting on the suspended sphere.

problem 6: Two identical charged spheres of mass 0.10 g are hung from similar point by silk threads. The electrostatic force between the spheres causes them to separate by 10 mm. The angle between one of the silk threads and the vertical is 5.7°.

a) By drawing a force diagram, determine the electrostatic force FE between the spheres.

b) Compute the size of the charge on each sphere.

c) The average leakage current from a charged sphere is 1.0 × 10^–11 A.  Compute the time taken for the spheres to discharge completely.

d) describe how the two spheres might be given identical charges.