problem 1:

a) How does the fact that the speed of light is constant lead to relativity of the simultaneity? Describe in around 250 words with the help of an illustration.

b) What is the speed of an electron (m_e = 0.511 MeV/c²) with a momentum of 100 MeV/c? What is the speed of a proton (m_p = 940 MeV/c²) with a momentum of 100 MeV/c?

c) At what speed is a particle’s kinetic energy equivalent to its rest mass energy?

problem 2:

a) A non relativistic particle is moving three times as fast as an electron. The ratio of the de-Broglie wavelength of the particle with respect to that of the electron is 1.813 × 10⁻⁴. Recognize the particle.

b) The speed of a bullet of mass 0.05 kg and the speed of an electron are measured to be the same, 300 ms⁻¹, with an uncertainty of 0.01%. With what accuracy would we measure the position of each, if position is measured concurrently with the speed in the experiment? Comment on the result.

c) Consider a particle of mass m which can move freely all along the x-axis between –a/2 ≤ x ≤ a/2 but is prohibited from going outside this region. The wave function for the lowest energy state is:

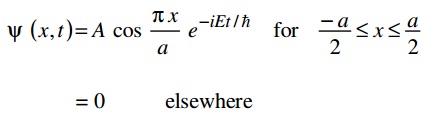
By using the time dependent Schrodinger Equation, find out the value of E for this lowest energy state.

d) Show that the product AB is not Hermitian, if A and B are Hermitian operators. Under what condition would AB be a Hermitian operator?

problem 3:

a) Compute the expectation value of the potential energy for the hydrogen atom in the state Ψ₂₁₀.

b) If the K, L and M energy levels of Platinum lie roughly at 78 KeV, 12 KeV, and 3 KeV, correspondingly, find out the approximate wavelengths of the Kα and Kβ lines. What minimum potential difference across an X-ray tube is needed to excite these lines?

c) Obtain the ground state spectral term for Sr³⁸.

problem 4:

a) The decay constant λ of a radioactive element is 0.00231 per day. Compute its half-life and average life.

b) Draw the binding energy curve exhibiting variation of binding energy per nucleon with mass number. With the help of this, describe the phenomena of nuclear fission and fusion.

c) describe the working of:

i) Wilson cloud chamber,
ii) Bubble chamber,
iii) Spark chamber, and
iv) Proportional chamber.

d) The mass of a proton and of neutron are 1.008142 and 1.008982 amu correspondingly. Compute the binding energy per nucleon of ¹⁶O nucleus.

[Take Atomic mass of ¹⁶O = 15.994915 amu]