problem 1
(a) Find the natural domain and determine the range of the following functions.
i. f (x) = √x2 - 3
ii. f (x) = 3sin x
(b) Sketch the graph of the function:
y = 1 + 2x - x2
by appropriately translating and reflecting the function y = x2
(c) Find expressions for
f (x) = x/1 + x2, g (x) = 1/x
Find the domains of both the compositions.
(d) Using the horizontal line test find which of the following functions f is one-to-one:
(i) f (x) = 3x + 2
(ii) f (x) = x
problem2.
(a) Find the value of:
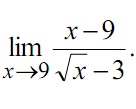
(b) Determine the value of:
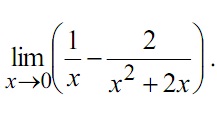
(c) (i) Find a value of the constant k, which will make the following function continuous.
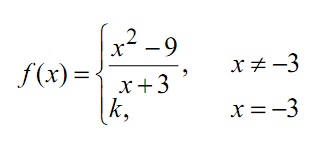
(ii) Sketch the continuous function.
(iii) Show that the continuous function can be written as a polynomial.
(a) Using the definition of the derivative, dx/df of a function f(x) with respect to x as:
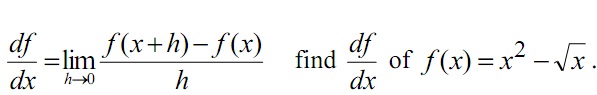
(b) Find dx/dy of: y = (3x2 + 2/x + 3)
(c) A car is driven down a street highway such that in the first 12 seconds it travels a distance s = 4.5t2 m from its initial position.
(i) Find the average velocity of the car over the time interval [0,12] s.
(ii) Find its instantaneous velocity at t = 6 s.
(d) A spherical balloon is to be deflated so that its radius decreases at a constant rate of 15 cm/min. At what rate (cm3/min) must air be removed when the radius is 9 cm?