problem1)

Determine the value of c (if any) so that the system of equations with the following augmented matrix

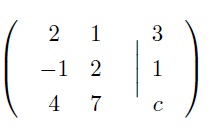
has the requested number of solutions. Make your rationale clear!
(a) No solution.
(b) Infinitely many solutions.
(c) Exactly one solution.
(d) Exactly two solutions.

problem2)

Find the inverse of the following matrix by using Gauss-Jordan elimination applied to (A|I). Please show all the details.

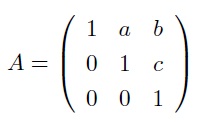
It’s a good idea to validate your answer by selecting sample values of parameters a; b; c and checking (using a calculator) that your calculations give a correct answer.

problem3). Using the result of problem 2, find the inverse of the matrix

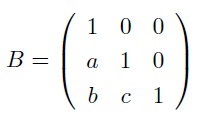
problem4) Give an ex of matrices A and B such that AB exists but BAdoesn’t.

problem5) Give an ex of a matrix A such tah A² = 0. (A² means AA).

Questio6) Show that if A is an n   n invertible matrix, there could be no nonzero n   n matrix B such that AB = 0.
HINT: Sometimes, when you need to show that something could not happen, a good way to argue is to suppose that it could and then arrive to a logical contradiction.

problem7) Find elementary matrices E₁ and E₂, such that U = E₂E₁A is upper triangular. Factor A into A = LU by finding inverses of E₁ and E₂.

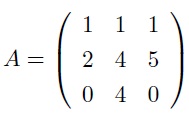
problem8) Consider A, L, and U from problem7, and let b=

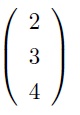
Solve the system Ax = b by solving the equation Ly = b first (using substitution). Once you find y, solve the equation Ux = y by back substitution.