Aim: To practice MATLAB and basic Simulation Techniques
problem) A gambler makes a series of plays with outcomes X1,X2....... where the Xi, i>=1 are independent, identically distributed random variables. The cost of each play is c. The gambler can stop at any time n>=1 with the fortune:
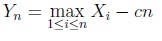
The gambler will stop if Xn > β. The gambler wants to maximize the mean of his fortune. What are the best values of β in the following two cases?
1) Case A: c = 0.2 and the distribution of Xn is the exponential distribution, i.e., its density function is
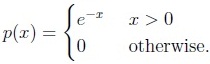
2) Case B: c = 0.1 and Xn is a discrete random variable obeying Poisson distribution:
P(x=k) = 1/ek! for k= 0,1,2,3....,
Your Task:
i) Find the best of values of β by using Monte Carlo simulation.
ii) prepare a report with the following sections:
• Problem: You should describe this problem in a way such that a 16-year old high student student can understand it.
• Method: You should describe and describe your method (not your matlab code) in details.
• Code: your well-structured and well-documented code.
• Experimental Results and Discussion: You report your ex-perimental results here and give some discussions. You should use figures to show your results.
• Conclusion: Summarize what you have done and your reection. Your report should be at most five pages.
Submissions:
1) On-line submission
2) Your submission should include:
a) your report (named by REPORTyourloginname.XXX) and
b) your code file (named by CODEyourloginname.XXX).