problem:
a) Given that k is a constant, find which of these equations are linear.
i) x1 – x2 + x3 = sin k,
ii) kx1 – (1/k) x2 = 9,
iii) 2k sinx1 – x2 + x32 = 0
b) Find the augmented matrix of the following system of linear equations:
2x1 + 2x3 = 1
3x1 – x2 + 4x3 = 7
6x1 + x2 – x3 = 0
problem:
a) Consider the following system of linear equations:
x + y + 2z = a
x + z = b
2x + y + 3z = c
Show that for this system to be consistent, the constants must satisfy the condition: c = a+ b
b) prepare the definition of a reduced-row-echelon form matrix. prepare which of the following matrices are in the row-echelon and which are in the reduced row echelon forms.
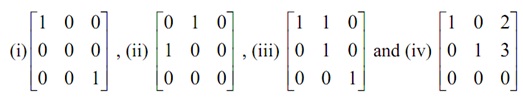
problem: Solve the following system of lonear equation by Gauss-Jordan elimination method.
x1 + x2 + 2x3 = 8
-x1 – 2x2 + 3x3 = 1
3x1 – 7x2 + 4x3 = 10
problem: Solve the following system of linear equations for λ = 1 and 2.
2x1 – x2 = λ x1
2x1 – x2 + x3 = λ x2
2x1 – 2x2 + x3 = λ x3