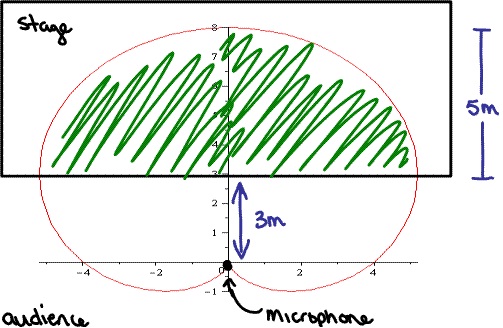
problem 1: When recording live performances, sound engineers frequently use a microphone with a cardioid pickup pattern since it suppresses noise from the audience. Assume that the microphone is placed 3 m from the front of the stage and the boundary of the optimal pickup area is given by the cardioid r = 4 + 4 sin θ, where r is measured in meters and the microphone is at the pole. The musicians want to know the area they will have on stage in the optimal pickup range of the microphone. Answer their problem.

problem 2: The temperature at a point (x, y, z) is given by T (x, y, z) = 200 e^-x2-3y2-9z2 where T is measured in ^oC and x, y, z are in meters.

a) Find out the rate of change of temperature at the point P (2, -1, 2) in the direction toward the point (3,-3, 3).

b) Find out the maximum rate of rise at P.

problem 3: Find out the local maximum and minimum values and saddle point(s) of the function f (x, y) = xy (1 – x – y)