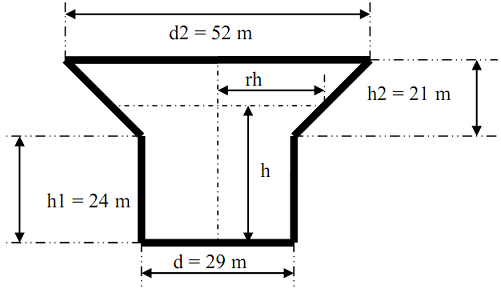
The tank in the water tower has the geometry shown in figure below (the lower part is a cylinder and the upper part is an inverted frustum cone).  Inside the tank there is a float that indicates the level of the water.
 You will be writing a function that determines the volume of the water in the tank from the position (height h) of the float.  This function will be called cs151sp13assn7 and there will be one input argument to the function that represents the height of the water in meters (this value could come in as a matrix of multiple water values).  There are no output variables for this function.

NOTE: You may be using if statements, the find function and the any function to help you with the steps outlined below.  There may be a combination of these commands or you may have a different way to solve it.  However, you may NOT use any loop commands to solve the problem.

A Step-by-step Procedure

1.  Create the correct function header as defined above.

2.  Check to see if there are any heights within the matrix that will cause the water to overflow the tank or if there are any values that are negative.  In either of these cases, your function should display an error message and stop processing.

3.  Find all the heights that are less than or equal to 24 meters.

4.  Print out how many values meet the criteria in step 3.

5.  If there are any values less than or equal to 24 meters, then find out the volume of these water levels using the equation: v = Π (14.5)²h.

6.  Print out these values using the fprintf command (see the ex below for what the output will look like – note that the height and volume values are printed out to two decimal places).

7.  Redo steps 3 through 6 for heights that are greater than 24 meters and use the volume equation: v = Π (14.5)² (24) + 1/3 Π (h – 24) (14.5² + 14.5r_h+r_h²) where r_h = 14.5 + 11.5/21 (h – 24).

ex Output

>> cs151sp13assn7([24 25 26 27 23 22 28 0 1])
There are 5 values below (and including) 24
For h = 24.00 m, the volume is 15852.48 m^3
For h = 23.00 m, the volume is 15191.96 m^3
For h = 22.00 m, the volume is 14531.44 m^3
For h = 0.00 m, the volume is 0.00 m^3
For h = 1.00 m, the volume is 660.52 m^3
There are 4 values above 24
For h = 25.00 m, the volume is 16538.26 m^3
For h = 26.00 m, the volume is 17275.81 m^3
For h = 27.00 m, the volume is 18067.03 m^3
For h = 28.00 m, the volume is 18913.79 m^3
>> cs151sp13assn7([25 26 27 28])
There are 0 values below (and including) 24
There are 4 values above 24
For h = 25.00 m, the volume is 16538.26 m^3
For h = 26.00 m, the volume is 17275.81 m^3
For h = 27.00 m, the volume is 18067.03 m^3
For h = 28.00 m, the volume is 18913.79 m^3
>> cs151sp13assn7([24 46 26 27 23 22 28 0 1])
Invalid values are in the matrix, please rerun function with valid values
>> cs151sp13assn7([45 24 0])
There are 2 values below (and including) 24
For h = 24.00 m, the volume is 15852.48 m^3
For h = 0.00 m, the volume is 0.00 m^3
There are 1 values above 24
For h = 45.00 m, the volume is 43632.79 m^3
>> cs151sp13assn7([45 -2 0])
Invalid values are in the matrix, please rerun function with valid values