1 Errors
a. Run the MATLAB script
sum = single(0); term = single(1);
n=1;
while sum + term > sum
sum = sum + term;
n=n+1;
term = 1/n;
end
n
Describe what you think it is trying to do. What would this code do in exact arithmetic? describe why the code produces a finite result and (harder) describe the output. What would happen (don't try it!) if you replaced the first line with sum=0; term=1;?
b. Use Taylor series to derive the form of the truncation error of the approximation
f'(x) =3f(x) -4f(x - h) + f(x -2h)/2h
assuming f ≡ C3. Given that the round off error has the same form as in the Forward Difference case, find an expression for the step size h that gives the smallest total (absolute) error. Modify ForwardDifference.m to show how the total error in using Equation 1 behaves for various values of h and comment on your results.
2 Operation counts
a. Derive the operation count (multiplications and divisions only) for
(i) Choleski factorization (without pivoting) A detailed algorithm for Choleski factorization can be found via the MAST30028 website on p. 78 of Heath's Lecture Slides --- Chapter 2.
(ii) Gauss elimination (equivalent to LU factorization) without pivoting of an Upper Hessenberg matrix. An Upper Hessenberg matrix is one with zeroes below the subdiagonal. Just modify the derivation for Gauss elimination.
(iii) solution of a tridiagonal system via LU factorization without pivoting (also called the Thomas algorithm) This is the algorithm implemented in the code tridisolve in the Asst1 folder on the server.
b. Verify qualitatively the running times you obtained above, by timing the solution of linear systems of size at least 1000X1000 with matrices having the appropriate structure (symmetric positive definite, Upper Hessenberg or tridiagonal).
Construct the matrices yourself with suitable MATLAB commands such as diag, triu, rather than using particular matrices from the MATLAB gallery.
For all cases, use \ to solve the system. For case c, try a tridiagonal matrix created with diag and one created with spdiags.
describe what you think is going on.
3 Application: Nonlinear systems of equations
You have met Newton's method as a method for solving nonlinear equations in the form f(x) = 0.
xn+1 = xn-f(xn)/f'(xn)
which gives iterates {xn} that converge rapidly to the solution x* provided the initial guess x0 is sufficiently close to x* . Applying this to the function
f(x) = x2 - a produces the iteration xn+1 = xn - x2n -a/2xn= xn/2 + a/(2xn)
which should look familiar. It can be written in the alternative form: solve in turn
f'(xn)sn = f(xn); xn+1 = xn - sn
For a system of two nonlinear equations f1(x1, x2) = 0; f2(x1,x2) = 0
or in vector notation
f (x) = 0
Newton's method generalizes in the following way: solve the 2X2 linear system
J(xn)sn = f (xn) then update xn+1 = xn - sn
where J is the Jacobian matrix formed from f
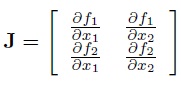
To get an idea how it works, try out the Java applet http://www.cse.illinois.edu/iem/nonlinear_eqns/Newton2D/
a. prepare a MATLAB function to implement Newton's method for a system of 2 nonlinear equations.
It should have the calling sequence [roots, count, resids, history] = ass1Q3(func,x0,tol)
where:
• the first input argument is a function handle to a function that returns the value of the function f and the Jacobian matrix J at the position x e.g. function [ f J] = ex2( xx )
The function ex2 needs to be written by the user, including the expressions for f and J. There is no need for J to be found symbolically from f .
• x0 is the initial guess ( a column vector)
• tol is the absolute tolerance. The iterations should stop once the residual ||f||, measured using the vector ∞-norm, is below tol.
• the first output argument is a column vector containing the solution x
• count is the number of iterations required
• resids is a vector containing the norms of the residuals at each iteration
• history is a matrix whose columns are the iterates xn i.e. each column is a 2X1 array.
The function should:
• use a default tolerance of 10-10 if none is given
• use a while loop but loop no more than 50 times.
Although I only need it to work for systems of 2 equations, you should be able to prepare it so that it can be used (in principle) on a system of any size. My code is less than 20 lines long.
b. prepare a driver function to test your code on ex 2 of the Newton2D Java applet. The driver should produce output such as
After 5 iterations, the roots are [1.61803 1.61803]
c. Modify your driver to find the solution to
3x31 + 4x22- 145 = 0; 4x21- x32+ 28 = 0
Show results for 2 different initial guesses: x0 = (2, 2),(2,-1).
For each case, plot the convergence history - the residual norms at each iteration - on a suitable plot and (on a different plot) the solution trajectory - the set of iterates xn.
Comment on your results.