1)  Three-person Problem of Points: Pascal, Fermat and their old friend Chevalier de Mere each put $10.00 into a pot, and agree to play a game which has rounds. Each player has the similar probability of winning each round. They agree to play till someone has won 10 rounds, and that person would get the entire pot. Though , they are forced to stop playing after Pascal has won 8 rounds, Fermat has won 7 rounds and Chevalier has won 9 rounds. How must they divide the pot?

2)a)

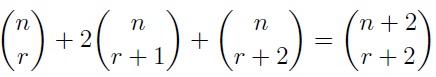
Demonstrate that  A counting proof could be fun? But any old proof would do. (Note that the coefficients (1,2,1) in the above are just the elements of the second row of Pascal’s triangle. In general, if you take any row of Pascal’s triangle and apply all of the coefficients to adjacent entries of a later row in the table, you would get another entry in Pascal’s triangle. You do not have to prove this).

b) Not connected to part a) above . Consider the two player Problem of Points set up, where the game consists of n rounds, and where player A has won a rounds and Player B has won b rounds (a, b < n) when they are forced to quit. Let r = 2n − 1 − (a + b). Demonstrate that according to Pascal-Fermat solution, the ratio of A’s share of the pot to B’s share of the pot must be:

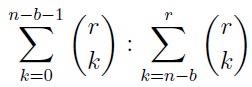
That is, all you required is the r’th row of Pascal’s Triangle to get the split of the pot, as pointed out by Pascal.

3) The elevator in the Math and Computer Building can stop at one of six floors. Four riders get on the elevator at the first floor and the elevator heads up. Each rider picks a floor at random (from floor 2 to floor 6) and gets of, and it is possible for more than one passenger to get of at any floor.

a) Describe, in words (no need to list all possibilities), S, the sample space for this experiment. Be sure to include the total number of points in S.

b) Assuming the points in S to be equally probable, find:

i) the probability that nobody gets off at the second floor.

ii) the probability that nobody gets off at the odd numbered floors

iii) the probability that half of the riders get off at the same floor and the other half get of at a different floor.

c) Generalize the results in i), ii) and iii) for r riders and n floors. Assume both r and n are even.

4) In an agricultural experiment, we wish to compare the yields of three different varieties of wheat. Call these varieties A, B and C. We have a field that has been marked into a 3X3 grid so that there are 9 plots available to plant the varieties. We randomly assign the varieties to the plots so that each variety appears 3 times in the grid.

a) How many several ways can the varieties be assigned to the plots?

b) Random assignment of varieties to plots is known as a completely randomized design. A better design may be to randomly assign the varieties so that each variety appears once in every row of the grid. This is called a randomized block design. How many possible randomized block designs are there involving 3 varieties and a 3X3 grid?

c) A third design will assign the varieties to the plots so that every variety appeared once in every row and once in every column of the grid. This is known as a Latin square design. How many possible Latin square designs are there involving 3 varieties and a 3X3 grid?

d) For r varieties and an rXr grid, how many designs of the first two types are there? (The number of Latin Squares of a given oder is an open problem - solve it to become famous!!).

e) For the first two designs (and the general case in d), what is the probability that at least one variety will appear in the same position in each row?

5) In a study of outcomes for patients who had been in the Intensive care Unit (ICU) at a large hospital, the records from last 150 patients who had been in the ICU for more than one day are obtained. The data for the number of patients in four categories is summarized in the table below.

CHD - Yes CHD-No Total
Stroke -Yes 52 8 60
Stroke-No 68 22 90
Total 120 30 150

So of the 150 patients, 120 were diagnosed with Coronary Heart Disease (CHD), 52 had both CHD and stroke, 68 had CHD but not stroke, etc. A patient record is selected at random. Let A be the event that the record is for an ICU patient who had CHD, and B be the event that the record is for a patient who had a stroke.

a) i) Are the events A and B independent? describe.

ii) Are the events A and B mutually exclusive? describe.

iii) Find P(AB).

iv) Find P(A U B).

b) For a detailed chart review, 50 of the 150 records are selected at random without replacement.

i) Find the probability that the sample contains 45 patients with CHD. (An expression is OK here, but try to do the calculation).

ii) Find the probability that the sample contains more than 45 patients with CHD or stroke. (An expression is OK here, but try to do the calculation).

6) In a three-cornered paint ball duel, A, B, and C successively take shots at each other till only one of them remains paint free. Once hit, a player is out of the game and gets no more shots. The three paint ballers have di↵erent probabilities of hitting their target. A hits the target 30% of the time, B hits the target 50% of the time and C (the brute) hits the target 100% of the time. A shoots first, followed by B, then C, then back to A if paint free, etc. If each player adopts the best strategy at each turn, including possibly an intentional miss, find the probability of remaining paint free for each of A, B, and C.

7) There are two diagnostic tests for a disease. Among those who have the disease, 10% give negative results on the first test, and independently of this, 5% give negative results on the second test.

Among those who do not have the disease, 80% give negative results on the first test, and, independently, 70% give negative results on the second test. Twenty percent of those tested actually have the disease.

a) If both tests are negative, what is the probability that person tested has the disease?

b) If both tests are positive, what is the probability that person tested has the disease?

c) If first test gives a positive result, what is the probability that second test would also be positive?

8) There are n seats on an airplane and n passengers have bought tickets. Unfortunately, first passenger to enter the plane has lost his ticket and, so he just selects a seat at random and sits in it. Thereafter, each of the remaining passengers enters one at a time and either sits in their assigned seat if it is empty, or, if someone is sitting in their seat, chooses a seat at random from those that are empty.

a) If n=2, what is the probability that last passenger to enter would end up sitting in her assigned seat?

b) If n=3, what is the probability that last passenger to enter would end up sitting in her assigned seat?

c) For general n>=2, what is the probability that last passenger to enter would end up sitting in her assigned seat? (We would need a proof here).