problem 1: Consider Efron’s non-transitive dice where the 6 faces as are in the table shown below:

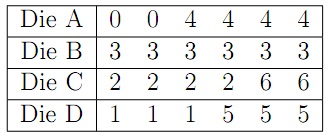
a) Assume that there are four players in the game and each will choose one die and roll it. The largest number will win. For each die, compute the probability that the largest number observed takes place on that die. Which die would you select?

b) Assume that there are four players in the game and each will select one die and roll it. The person who rolls the smallest number will be removed. For each die, compute the probability that the smallest number observed takes place on that die. Now which die would you select (supposing you want to stay in the game instead of reading a good book, having root canal work, and so on)?

c) Assume that in the four player game, the person who rolls the smallest number pays $5.00to the person who rolls the largest number. Compute each player’s expected gain after one round.

d) Assume that the person with die A loses the ?rst round and is removed. The three players play another round with only dice B, C, and D. Again, the person who rolls the smallest number pays $5.00 to the person who rolls the largest number. Compute each player’s expected gain from this round.

e) Assume the person with die D loses the ?rst round and is removed. The three players play another round with only dice A, B, and C. Again, the person who rolls the smallest number pays $5.00 to the person who rolls the largest number. Compute each player’s expected gain from this round.

problem 2: The probabilities for five discrete distributions that we have discussed can be find outd recursively.

In other words, if X is a random variable with probability function f_X(x)= P(X = x), then f_X(x)/f_X(x-1) = g(x), where g(x) may also contain parameters of the distribution, and fX(x-1) = 0. This can be a way to produce the probabilities in case functions like (ⁿ_x) are not available. You start by computing P(X = minimum of the range of X) and get the rest recursively.

a) Find g(x) for the Poisson distribution with parameter λ.
b) Find g(x) for the Binomial distribution with parameters n and p.
c) Find g(x) for the Hyper geometric distribution with parameters a, b, n and N = a + b.
d) (Will this never end)? Find g(x) for the Negative Binomial distribution for X, the number of trials until the rth success in a sequence of Bernoulli trials with P(S) = p.

problem 3: For a research study on smoking cessation, we require a sample of 25 smokers from a population of 24,000 undergraduates. Suppose there are 2,880 smokers and 21,120 non-smokers in the population.

a) Let X is a random variable giving the number of smokers in a simple random sample of 200 from the population (chosen without replacement, of course). Provide an expression for P(X = 25).

b) Assume that we want to sample until we have obtained 25 smokers. Let Y be a random variable giving the number of people we must sample (without replacement) to obtain 25 smokers. Give an expression for P(Y = 220).

c) Strati?ed Random Sample in 24,000 people in the population, there are 14,000 males of whom 1920 smoke, and 10,000 females of whom 960 smoke. We decide to take a sample of 120 males and 80 females (at random without replacement). Let Z_M and Z_F be random variables giving the number of male smokers and female smokers in the sample. Provide an expression for P(Z_M + Z_F =25).

d) Assume we do the strati?ed random sampling as in c). If our sample contains 25 smokers, what is the probability that 14 of the smokers will be males? An expression is ?ne here.

problem 4: The safe level of total coliform bacteria in well water is 5 or fewer bacteria per 100 ml. Then one rule for declaring a sample to be ”safe” is if a 20 ml sample contains 0 or 1 bacteria. Assume coliform bacteria in well water are distributed according to a Poisson process at an average concentration of λ per 100 ml, and let X be a random variable giving the number of coliform bacteria in a 20 ml sample of well water.

a) If λ = 10 (twice the safe limit), what is the probability a 20 ml test tube will contain 0 or 1 bacteria (and so the sample will be declared”safe”)?

b) Regulations require that three consecutive samples taken one week apart all have to be ”safe” in order to declare the well ”safe”. If λ =10 each week, what is the probability that all three 20 ml samples will show 0 or 1 bacteria?

c) A 200 ml container is used to collect a larger sample and this sample is transferred to ten 20 ml test tubes for analysis. If λ =10 and the200ml sample contains 20 bacteria, derive the probability distribution for Y, the number of bacteria in the ?rst test tube. Name the probability distribution for Y, and give E(Y) and Var (Y).

d) The regulators feel that the current regulations requiring 3 safe samples taken a week apart are not protective enough if λ =10.They are thinking of changing the rules to either defining a safe sample as one with 0 bacteria and requiring a safe sample each week for three weeks, or keeping the definition of a safe sample as it is but requiring a safe sample each week for n weeks. Find the smallest value of n so that, if λ =10,

P(declare a sample safe under Rule 2) < P(declare a sample safe under Rule 1)

problem 5: An airline knows that there is a 95% chance that any passenger for a commuter flight that will hold 189 passengers will show up, and assumes passengers arrive independently of one another. The airline decides to sell n = 199 tickets to reduce the number of empty seats, expecting 5% of the passengers not to show up. Let X be a random variable giving the number of people who show up for the flight, and let Y = X - 189 be a random variable for the difference between the number of passengers who show up and the number of seats on the plane.

a) Give expressions for E(X), Var(X), E(Y), Var(Y).

b) Give an expression for P(Y> 0). What do you think of their choice to sell 199 tickets?

c) They conduct a review of their policies and decide that they do not want the bad public relations associated with passengers with tickets not getting a seat. So they hire you as a consultant at an exorbitant fee to give them advice. After you probe, you learn that as long as they have enough seats for passengers with tickets 98% of the time, they will accept the risk. What is the largest value of n so that P(Y> 0) ≤ 0.02?

d) Briefly describe why the Bernoulli process assumptions might not hold here.

problem 6: Let X be a hyper geometric random variable giving the number of supporters of a bylaw in a sample of n individuals sampled without replacement from a population of size N that contains a supporters of the bylaw and b non-supporters of the bylaw (N = a + b).

a) Find E(X) and E(X(X - 1)).

b) If n =50, a =140, and b = 860 so that N =1000, give a numerical value for Var(X). Verify numerically that Var(X) = (na/N)(1 - a/N)(1 - (n - 1)/(N - 1)).

c) If we were to use the binomial approximation to the distribution of X, give the approximate values for E(X) and Var(X).

d) If we were to Poisson approximation to the binomial distribution to approximate the distribution of X, give the approximate values for E(X) and Var(X).

e) Give the exact and the two approximate values for P(X =14) in the above ex.

f) Give the exact and approximate values for P(X =2), when n =50, a =20, and b =980 (N =1000).

g) Comment briefly on the adequacy of the approximations in e) and f) and give reasons for why they might or might not be suitable.

problem 7: Let X be a geometric random variable giving the number of trials until the ?rst success in a sequence of Bernoulli trials where P(S) = p on any trial, so fX(x) = (1 - p)^x-1p, for x = 1, 2, 3,....

a) Find the moment generating function, M_X(t), for X, and use this to find K_X(t)the cumulant generating function for X.

b) Using either M_X(t)or K_X(t), show that E(X) =1/p and Var(X)=(1 - p)/p².

c) Let Y be a random variable giving the number of failures before the ?rst success in the same Bernoulli process. Using the fact that Y = X-1 and the results of parts a) and b), derive M_Y(t), E(Y), and Var(Y).

problem 8: Let X_n be the number of ascending sequences in a random permutation of the integers {1,2, . . . ,n}. For ex, the number of ascending sequences in the sequence 2, 1, 3, 5, 4, 6 is three since 2, 1, 3, 5 and 4, 6formascendingsequences.Inthisex, neither1, 3 nor 3, 5 are considered ascending sequences since they are part of a longer ascending sequence. Define p_n(k)= P(X_n = k), with p_n(0) = 0 and p_n(n + k) = 0 for k > 0.
a) Find p₁(1), p₂(1), and p₂(2).

b) describe (briefly) why p_n(1) = p_n(n)=1/n!.

c) Derive p₃(2).

d) Show that the following recursion for the probabilities p_n(k) holds

p_n(k)= (k/n) p_n-1(k)+ [(n - k +1)/n] p_n-1(k -1).

and use this to generate p₄(k) = P(X₄ = k) for k = 1, 2, 3, 4.

e) In going from n-1 integers to n the number of ascending sequences can either increase by 1 or stay the same. Give an expression for the probability that the number of ascending sequences increases by 1, and find out this probability for n = 2, 3, 4. Hence give a conjecture for the expected number of ascending sequences in a random permutation of the integers 1, 2,...,n.