Particles incident from the left are confronted with a step in potential energy as shown in Figure. The step has a height U, & the particles have energy E > U. Classically, we would expect all of the particles to continue on, although with reduced speed. According to quantum mechanics, a fraction of the particles are reflected at the barrier.

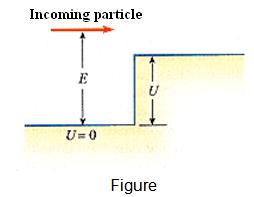
[A] Prove that the reflection coefficient R for this case is as follows, where k1 = 2π / λ1 & k2 = 2π / λ2 are the angular wave numbers for the incident & transmitted particles.

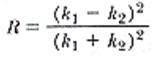
Proceed as following: Show that the wave function Ψ 1 = A cos k1x + B cos ( -k1x) satisfies the Schrodinger equation in region 1, where x < 0. Here A cos k1x represents the incident beam, & B cos (-k1x) represents the reflected particles. Show that Ψ 2 = C cos k2x satisfies the Schrodinger equation in region 2, for x > 0. Impose the boundary conditions Ψ 1 = Ψ 2 & dΨ 1/dx = dΨ 2/dx at x = 0, to find the relationship between B & A. Then evaluate R = B2/A2.

[B] A particle that has kinetic energy E = 6.00 eV is incident from a region where the potential energy is zero onto one in which U = 4.50 eV.
a. Compute its probability of being transmitted.
b. Compute its probability of being reflected.