Question: Suppose the relative growth rate is a linear function of population at time t by using the formula. Demonstrate the steps to compute the relative growth rate when P = 5.3 and when p= 7.2
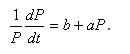
| Time |
T |
Population |
symmetric difference quotient |
Relative Growth Rate |
| 1790 |
0 |
3.9 |
|
|
| 1800 |
10 |
5.3 |
0.165 |
|
| 1810 |
20 |
7.2 |
0.215 |
|
| 1820 |
30 |
9.6 |
0.285 |
|
| 1830 |
40 |
12.9 |
0.375 |
|
| 1840 |
50 |
17.1 |
0.515 |
|
| 1850 |
60 |
23.2 |
0.715 |
|
| 1860 |
70 |
31.4 |
0.83 |
|
| 1870 |
80 |
39.8 |
0.94 |
|
| 1880 |
90 |
50.2 |
1.155 |
|
| 1890 |
100 |
62.9 |
1.29 |
|
| 1900 |
110 |
76 |
1.455 |
|
| 1910 |
120 |
92 |
1.485 |
|
| 1920 |
130 |
105.7 |
1.54 |
|
| 1930 |
140 |
122.8 |
1.3 |
|
| 1940 |
150 |
131.7 |
1.425 |
|
| 1950 |
160 |
151.3 |
2.38 |
|
| 1960 |
170 |
179.3 |
2.6 |
|
| 1970 |
180 |
203.3 |
2.36 |
|
| 1980 |
190 |
226.5 |
2.27 |
|
| 1990 |
200 |
248.7 |
2.745 |
|
| 2000 |
210 |
281.4 |
|
|