1. Evaluate the given limits, showing all working:

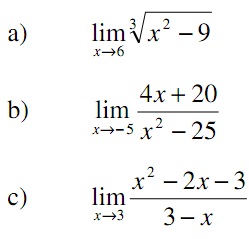
2. Using first principles (i.e. the method used in ex 1, Washington 2009, Section 23.3 – Using definition to find derivative) find the derivative of each function and then evaluate the slope of the tangent line at the given point.

a). y = 12x² - x³; (1, 11)

b). y = x/x - 1; (-3, 3/4)

3. The cross section of a hill can be approximated by the curve of y = 0.3x – 0. 00003x³ from x = 0 to x = 100 m. The top of the hill is level. How high is the hill?

4. A rectangular solid block of ice is melting such that the height is always twice the edge of the square base. Find the expression for the instantaneous rate of change of surface area A with respect to the edge of the base e.

 5. a) During each cycle, the vertical displacement s of the end of a robot arm is given by s = (t² - 6t)(2t² - t + 1) where t is the time. Using the product rule find the expression for the instantaneous velocity of the end of the robot arm. 

b) The amount n (in g) of a compound formed during a chemical change is n = 8t/2t² + 3, where t is the time (in s). Find dn/dt for t = 3.0 s using the quotient rule.

6. The displacement s (in m) of an object as a function of time t (in s) is given by s = ³ √4 +9t
Using the Chain Rule find the values for:

i) The initial velocity.
ii) The velocity at t = 3 s.
iii) The initial acceleration.
iv) The acceleration at t = 3 s.

7.  a) A lens is described by the ellipse x² - xy + y² = 7 Use implicit differentiation to find the slope of a light ray tangent to the lens at  (1, −2 ).

b) Find the derivative of  x sec y - 2y = 2sin x cos x= −  without using a calculator.
 
b) Differentiate y = In(2x - 1/1 + x²)  without using a calculator.

8. For each of the following find:

i) The gradient of the graph at a given point
ii) The equation of the tangent line at that point
iii) The equation of the normal line at that point

a) y = 4x³ at the point (2, 32)

b) y = 1/2x at x = 1/4

9. a)  The distance d that can be seen from horizon to horizon from an airplane  varies directly as the square root of the altitude h of the airplane. If d = 213 km for h = 3950 m, find d for h = 5250 m.

b) The volume V of a given mass of gas varies directly as the temperature T and inversely as the pressure P. If V = 250 cm³when T = 200^°

C and P = 130 kPa, what is the volume when T = 170^°C and P = 130 kPa?

c) The acceleration of gravity g on a satellite in orbit around the earth varies inversely as the square of its distance r from the centre of the earth. If g = 8.7 m/s² for a satellite at an altitude of 400 km above the surface of the earth, find g if it is 1000 km above the surface. The radius of the earth is 6.4* 10⁶ m.

10. The time t required to test a computer memory unit is directly proportional to the square of the number n of memory cells in the unit. For a particular type of unit, n = 6400 for t = 25.0 s. Find the instantaneous rate of change of t with respect to n for this type of unit for n = 8000.