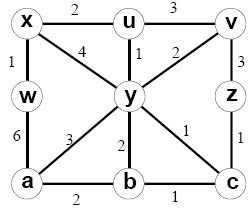
1. Consider the following network ex. With the indicated link costs along each link in the figure, use Dijkstra's shortest-path algorithm to find out the shortest path from x to all network nodes. Demonstrate how the algorithm works by computing a table.

2. Consider following network ex. Assume that the distance vector (DV) routing algorithm is used to find out the distance between nodes.

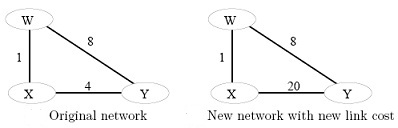
(a) Show the procedure of nodes X, Y and W find outs their Distance Vector for network illustrated by first Figure i.e., original network, i.e., link costs are C(xw)=1, C(xy)=4, and C(yw)=8.

(b) Suppose that after the DV is find outd by all nodes, the link cost of xy changed from 4 to 20. Demonstrate the procedure of nodes X, Y and W updates their Distance Vector for network illustrated by second Figure , i.e., link costs are C(xw)=1, C(xy)=20, and C(yw)=8.

3. We studied Dijkstra’s link-state routing algorithm for calculating the unicast paths which are individually the shortest paths from the source to all destinations. The union of these paths may be thought of as forming a shortest path tree. If each links has an associated cost and the cost of a tree is the sum of the link costs, then a spanning tree whose cost is the minimum of all of the spanning trees is known as a minimum spanning tree. Both shortest path tree and minimum-spanning tree could be used for broadcast routing. By constructing a counter ex, Demonstrate that the least-cost path tree is not always the same as a minimum spanning tree.