problem 1: The Power Method is a classic numerical algorithm for determining the largest eigenvalue and eigenvector associated with a matrix A. prepare a MATLAB function that returns the largest eigenvalue and eigenvector by using the Power Method (see Wikipedia) for a given matrix A. Construct the algorithm so that it always runs 100 iterations {you must not implement a stopping criteria. Don’t copy others codes. Test your algorithm on the matrix: A = [2.0, 0.2, 1.0; 0.2, 4.0, 1.3; 0.0, 1.3, 3.0] by using an initial eigenvector guess of b = [1; 1; 1].

problem 2: In class, we derived and resolved a model of a non-isothermal, insulated, CSTR with an exothermic reaction (model6.m). Want to derive and solve a very similar model of a system with only a single feed stream and the given properties:

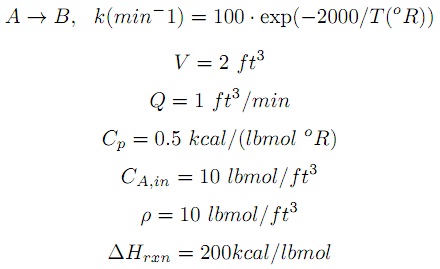
Simulate this system for 20 minutes with an initial concentration of C_A(0) = 10 lbmol/^oR and T(0) = 200^oR or T(0) = 600^oR. Compare and elucidate the steady-state result for the two different initial conditions. What is the significance of this result for implementing a process control scheme?

problem 3: Derive and resolve a model of an insulated water tank with a changing level (that is, changing tank volume). There is only one inflow stream with a flow rate of 1 kg/sec for t < 0 and 0.9 kg/sec for t ≥ 0.The out flow rate depends upon the level, H, within the tank and is given by m_out = kv√H where kv = 0:8 kg/(m^0.5s). The tank is fitted with an electric heater that inputs Q = 100kW (constant) and the cross-sectional area of the tank is 1.1m². Derive both the mass and energy balances, determine the steady state conditions at t < 0, and determine via numerical simulation the impact of the changing in flow rate at t ≥ 0.