problem 1: Solve the following grouping problem using the DCA method.

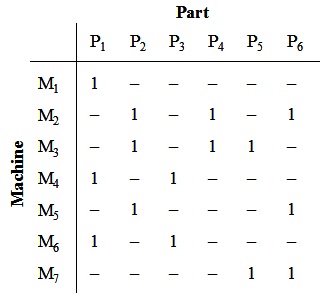
problem 2: Use the ROC methodfor the previous problem.

problem 3: Use the MIP method for the problem above assuming a total of 3 cells and no more than 4 machines per cell.

problem 4: Solve the problem in page 346 of the paper on cell formation by Boctor using the MIP method. Use 4 cells and no more than 3 machines per cell.

problem 5: Solve the problem using the MIP method and report the flow-distance score of the layout. There are no building restrictions. 

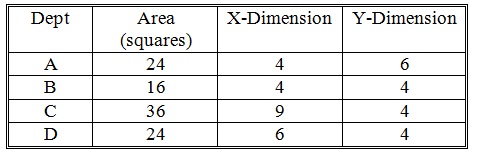
Assume the following dimensions for the departments.

problem 6: Solve problem above again and report the flow-distance score of the layout, now assuming that the X- and Y- dimensions of department C are interchangeable, as necessary.

problem 7: You are given the following flow-between matrix for a six department layout problem:

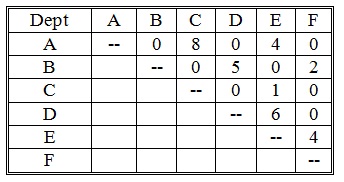
Solve the problem using the MIP method.  Assume that departments A and F have to be 2 x 2. Departments C and D could either be 2 x 3 or 3 x 2. Departments B and E may be 2 x 4 or 4 x 2. Draw the optimal layout and find the resulting flow-distance score. 

problem 8: Solve the following 8-department problem using the MIP method. What is the resulting layout and flow-distance score? Note that the aspect ratio of each department should be 2.

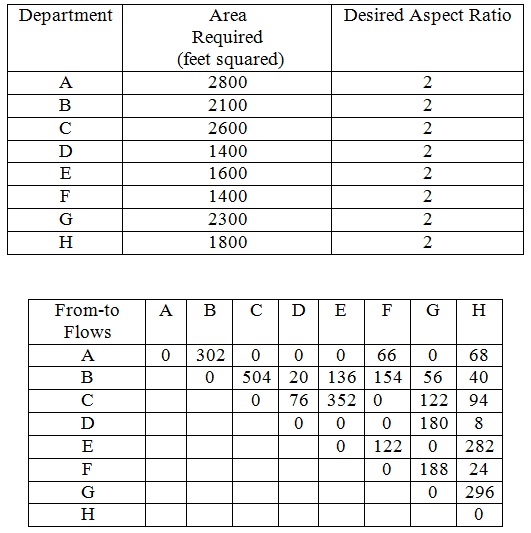
problem 9: Solve problem 8 with the condition that the resulting building should be compact. Assume the same penalty value in the objective function for Bx and By and draw your layout for the assumed penalty. 

problem 10: Assume that you have been asked to solve problem 8 with exact area constraints, the area error being no more than 1% for each department. What are the linear equations you would need for department G, assuming that the aspect ratio of G is no more than 2?

problem 11: Solve problem 8, with exact area constraint for all departments (the area error should be no more than 1%). Assume that the aspect ratio for all departments is no more than 2.