problem 1: Translate the given formula into a prefix form expression in Scheme:

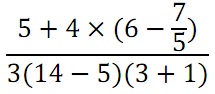
problem 2: Define a procedure which takes three numbers as arguments and returns the sum of the squares of two larger numbers.
 
problem 3: Consider the given mathematical function:

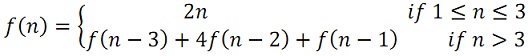
(a) prepare a procedure which computes f by means of the recursive process.
(b) prepare a procedure which computes f by means of the iterative process.
 
problem 4: Each of the given two procedures defines a method for adding two positive integers in terms of procedures inc, which increments its argument by 1, and dec, which decrements its argument by 1:

(define (plus1 a b)
(if (= a 0)
b
(inc (plus1 (dec a) b))))
 
(define (plus2 a b)
(if (= a 0)
b
(plus2 (dec a) (inc b))))
 
By using the substitution model, describe the process generated by each procedure in evaluating (+ 2 5). Are such processes iterative or recursive?
 
problem 5:

a) prepare a recursive procedure (digits n) which computes the number of digits in the integer n by using a linear recursive process. For illustration, (digits 42) must return 2 and (digits 13579) must return 5.

b) Reprepare (a) in such a way that a linear iterative process is produced. Call the procedure digits-it.

c) By using the substitution model, illustrate that your procedure in (b) generates a linear iterative process.
 
problem 6: Simpson's Rule is a more accurate method of numerical integration. By using Simpson's Rule, the integral of a function f between a and b is approximated as:

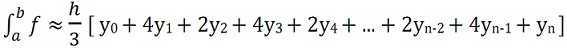
where  h = (b  -  a)/n, for some even integer n, and y_k= f(a + kh). (Increasing n increases the accuracy of the approximation.)

Define a procedure which takes as arguments f, a, b, and n and returns  the value of the  integral, computed by using Simpson's Rule. Use your process to integrate cube between 1 and 2  (with n = 100 and n = 1000)