problem 1: Show the result of the following sequence of UNION operations using union-by-weight with the following assumptions:

A) Unions are performed on the representatives on the sets that contain the arguments.

B) If the sets have the same weight, make the representative of the second argument point to the representative of the first argument.

C) The universe of elements is the integers 0 - 16:

a) Union( 3, 5 )        b) Union( 1, 7 )
c) Union( 3, 6 )        d) Union( 8, 9 )
e) Union( 1, 8 )        f) Union( 3, 10 )
g) Union( 3, 11 )      h) Union( 3, 12 )
i) Union( 3, 13 )       j) Union( 14, 15 )
k) Union( 16, 0 )      l) Union( 14, 16)
m) Union( 1, 3 )       n) Union (1, 14 )

problem 2: Answer the problems about the graph below:

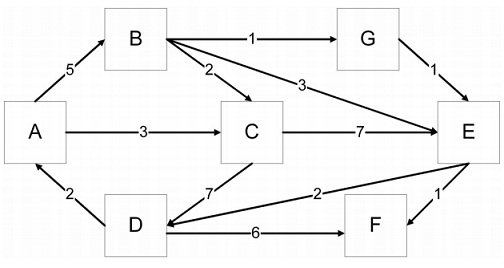
a) Name one cycle that begins and ends at B.

b) True/False – the graph is strongly connected.  If not, describe why not.

c) Find the shortest weighted paths from A to all other vertices. Your answer must include a list of all the vertices in order starting from A in each path and the weight of each path.