problem 1: Let G = (V,E) be a graph for which all nodes have degree 5 and where G is 5-edge is connected.

a) Show that the vector x which is indexed by the edges E and for which x_e= 1/5 for all e in E is in the Perfect Matching Polytope P^PM.

b) Use your result in a) to show that G must have a perfect matching.

c) Show that b) may not be true if G is only 1-edge connected (but still has degree 5 everywhere) by giving an ex of such a graph G which has no perfect matching.
 
problem 2:

a) Find the shortest paths from r to all other nodes in the digraph G = (V,E) shown below using the Bellman-Ford algorithm (as taught in class). Please show your work, and draw the final shortest dipath tree on a copy of a diagram of the digraph.

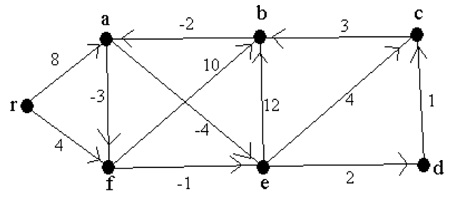
b) Using the potential y found in a), find a new set of costs c* for G which are non-negative, and preserve shortest dipaths.  

problem 3: Demonstrate that Dijkstra’s algorithm does not necessarily work if some of the costs are negative by finding a digraph with negative costs (but no negative cost dicircuits) for which it fails. You must also demonstrate that Dijkstra’s algorithm fails on your ex.
 
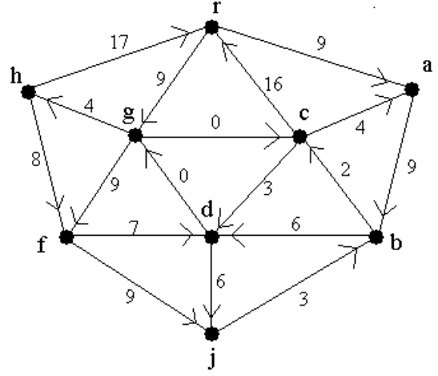
problem 4: Find a minimum cost spanning arborescence rooted at r for the digraph shown below, using the final algorithm shown in class. Please show your work, and also give a final diagram which shows your solution on the digraph, and states its final cost.

problem 5:

a) Given a digraph G = (V,E), prove that if we add a constant k to the length of every arc coming out from the root node r, the shortest path tree remains the same. Do this by using potentials: 

i) Show there is a potential y* for the new costs for which the paths in the tree to each node v have cost  y*v, and

ii) describe why this proves it. What is the relationship between the shortest path distances of the modified problem and those of the original problem? 
 
b) Can adding a constant k to the length of every arc coming out from a non-root node produce a change in the shortest path tree?  Justify your answer.
 
problem 6: Normally a potential y satisfies y_r = 0 and 0  ≥ y_w – c_vw –y_v. Given an integer K ≥ 0, define a K-potential to be an array y that satisfies yr = 0 and K ≥ y_w – c_vw –y_v. Show that for a K-potential y we have that for each node v, y_v is within K_n of being the cost of an optimal r-v dipath, i.e. show c(P) + K_n ≥ y_v for any r to v dipath P in G.