problem) Show that the following two grammars are equivalent:

Grammar 1: S → abAB | ba

A → aaa

B → aA | bb

Grammar 2: S → AbAaA | abAbb | ba

A → aaa

problem) Show that the following grammar is ambiguous:

S → aSb | SS | Λ

problem) The nor of two languages is defined as follows:

A word is in nor (L1, L2) if it is in neither L1 nor L2. If L1  and L2 are regular, show that nor (L1,L2) is also regular.

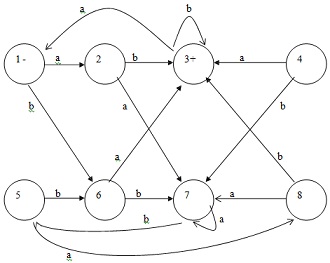
problem) Minimize the following DFA:

problem) Devise an NPDA to recognize the language   a^mbⁿ   where m=n or m=2n

problem)

a) Show a derivation tree for the string aabbbb with the grammar:

S → AB | Λ

A → aB B → Sb

(b Describe the language generated by this grammar.

problem) using the CYK algorithm, determine whether the word aab can be generated by the following grammar:

S → AB

A → BB | a

B → AB | b

problem) A 2-track TM contains binary number (k) on track 1. Outline the operation of a TM that halts with heads over cell k on the tape. The first cell is numbered 0.

problem) Suppose we restrict a TM so that it is not allowed to prepare the symbol that it reads; in other words in the quintuple ( Qi, X,  Qj, Y, Direction) X cannot be the same symbol as Y. Does this limitation reduce the power of the TM? Give reasons for your answer.

problem) A TM tape contains a binary number with an odd number of digits. prepare a TM that Halts if the middle digit is 0 and crashes otherwise.

problem) For each of the following, circle TRUE if the statement is always correct. Otherwise, circle FALSE.

(a) TRUE   FALSE               If L1  and L2  are nonregular languages than L1  ∩ L2 must be nonregular.

(b) TRUE    FALSE            If L is a nonregular language then L must be infinite.

(c) TRUE   FALSE          If a regular expression contains a Kleene star then the language generated by the regular expression must be infinite.

(d) TRUE  FALSE            If L is a regular language then L' must be a nonregular language.