Q1. Many other probability inequalities exist besides the Markov and Chebyshev's inequalities we saw in Chapter 4. For instance:

Gauss Inequality:

For a unimodal random variable X with mode ν and τ² = E(X - ν)², we have:

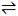
Vysochanskii-Petunin Inequality:

For a unimodal random variable X, for any arbitrary point α with ξ² = E(X - α)², we have:

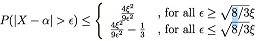
Compare (i.e. are they tighter/conservative/etc) the bounds obtained from Gauss, Vysochanskii-Petunin and Chebyshev's inequalities for:

(a) a random variable X following the uniform distribution in [0, 1]

(b) a random variable X following N(μ, 1).

Q2. If Z is a standard normal random variable, then

P(|Z| ≥ t) ≤ √(2/π) e^{-t^2/2}/t, for all t > 0.

(a) Prove the above inequality and its companion

P(|Z| ≥ t) ≥ √(2/π) (t/1+t²)e^{-t^2/2}.

Hint: start with working out the P(Z ≥ t).

(b) Compare the above inequality with Chebychev's inequality. You can illustrate the comparison giving specific examples by setting for instance t = 2 or any t of your choice.

Q3. (a) Let X₁, . . . , X_n be independent and identically distributed random variables with mean μ_x and variance σ²_X. Similarly let Y₁, . . . , Y_n be independent and identically distributed random variables with mean μ_Y and variance σ²_Y. Show that the distribution of the random varaible

W_n = (X^- - Y^-) - (μ_X - μ_Y)/√((σ²_X+ σ²_Y)/n)

converges to a standard normal distribution as n → ∞.

(b) The social media usage of two UCD students, Walter and Jesse, is to be compared. Walter's usage (in hours) is recorded for n_w = 50 randomly selected days and Jesse's usage is recorded for n_j = 60 randomly selected days. Assume that σ²_W = 0.5 and σ²_J = 0.3. Find the probability that the difference in the sample means will be within 0.1 hours of the difference between the population means.

Hint: The result shown in part (a) also holds when the sample sizes are unequal:

((X^- - Y^-) - (μ_X - μ_Y))/√(σ²_X/n_X + σ²_Y/n_Y) ∼ N(0, 1) as n_X, n_Y → ∞

(c) If n_W = n_J = n, find the smallest sample size n which will allow the difference between the sample means to be within 0.1 hours of the difference between the population means with probability greater than 0.9.

Q4. Let X₁, . . . , X_n be iid random variables with probability density function

f_X(x) = θx^θ-1, 0 ≤ x ≤ 1  0 < θ < ∞

 (a) Find the method of moments estimator for θ.

(b) Find the maximum likelihood estimator for θ.