Problem 1: Let k ≥ 32 be a positive integer, and let n =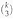. Consider the k x n binary matrix G whose columns are all the 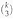binary vectors of length k and hamming weight 3. Let C be the (n, k, d) binary linear code generated by G. What is the minimum distance d of C? Prove your answer.

Hint: Let x ∈ C be the sum of some s rows of G. Consider the weight of x as a function of s.

Problem 2: In this problem, we use the term perfect code to refer specifically to an (n, M, d) binary code (either linear or nonlinear) with u = 2^m - 1, M = 2^n-m and d = 3, for an integer m ≥ 3. An extended perfect code C* is a code of length n + 1= 2^m obtained from a perfect code C of length n by appending an extra coordinate, so that the weight of all the code words in C* is even.

a. Let C ⊂ F₂ⁿ be a perfect code. Prove that there exists a partition C₀, C₁, . . . , C_n of F₂ⁿ into perfect codes, where C₀ = C and C_i = a_i + C is a translate of C for i = 1, 2, . . . , n.

b. Let E₂ⁿ⁺¹ be the set of all even weight vectors in F₂ⁿ⁺¹. Show that, given an extended perfect code C* ⊂ E₂ⁿ⁺¹, there exists a partition C*₀, C*₁, . . . , C*_n, of E₂ⁿ⁺¹ into translates of C*, with C*₀ = C*.

c. Let C₀, C₁, . . . , C_n and C*₀, C*₁, . . . , C*_n be partitions of F₂ⁿ and F₂ⁿ⁺¹ as in parts (a) and (b) above. Let π be an arbitrary permutation on the set {0, 1, . . . , n}, and let (a|b) ∈ F₂²ⁿ⁺¹ denote the concatenation of a ∈ F₂ⁿ⁺¹ and b ∈ F₂ⁿ. Prove that the code ϑ defined below is perfect:

ϑ =^def {(c*|c) : c*∈ C*_i, c ∈ C_j,  π(i) = j}

d. Use the construction in part (c) to show that, for all m ≥ 4, there exist nonlinear perfect codes of length n = 2^m - 1.

e. Prove that there are at most 2^{m2^n-m} distinct perfect codes of length n = 2^m - 1. Here, codes C and C' are considered distinct if the set of codewords of C differs from the set of codewords of C'.

Problem 3: The decay function D from F_qⁿ to F_q^n-1 is defined as follows. Each vector x = (x₁, x₂, . . . , x_n) in F_qⁿ is mapped by D into the vector:

D(x) = (x₂ - x₁, x₃ - x₂, . . . , x_n - x_n-1)

The lifespan of a vector x ∈ F_qⁿ is defined as the smallest integer i such that Dⁱ(x) = 0; that is, applying the decay function D to x successively i times results in the all-zero vector of length n - i. If no such i exists, then the lifespan of x is defined to be n. The lifespan of the vector 0 is zero, by convention.

a. Prove that if x₁ is a vector of length n and lifespan i, and x₂ is vector of length n and lifespan j, with j < i, then x₁ + x₂ is a vector with lifespan i. That is

lifespan (x₁ + x₂) = max {lifespan (x₁), lifespan (x₂)}

b. Suppose it is known that the lifespans of the k vectors x₁, x₂, . . . , x_k ∈ F_qⁿ are are all distinct. Prove that these k vectors are linearly independent over F_q.

c. Let ∝ be a primitive element of F_q, and let x₁ and x₂ be two vectors of lifespan i in F_qⁿ. Prove that there exists an integer j ∈ {0, 1, . . . , q-2} such that lifespan (x_i + ∝jx₂) < i.

d. Given a linear code C of length n and dimension k over F_q, let L_i denote the number of codewords of lifespan i in C. The integers L₁, L₂, . . . , L_n are called the lifespan distribution of C. Prove that the lifespan distribution of any such code C contains exactly k nonzero values.

e. Define the cyclic decay function D' from F_qⁿ to F_qⁿ as follows. Each vector x = (x₁, x₂, . . . , x_n) in F_qⁿ is mapped by D' into the vector:

D'(x) = (x₂ - x_i, x₃ - x₂, . . ., x_n - X_n-1, x₁ - x_n)

The lifespan with respect to this function is defined as before. Namely, cyclic-lifespan (x) is the smallest integer i such that applying the cyclic decay function D' to x successively i times results in the all-zero vector of length n. In this part, assume that n is a power of 2 and q = 2. How many binary vectors of length n and cyclic lifespan i are there, for each i = 0, 1, . . . , n?

Problem 4: In this problem, we deal with three different finite fields: the ground field GF(q), its extension GF(q^m) of degree m, and the extension of GF(q^m) of degree n, namely the finite field GF(q^mn). Throughout this problem, assume that n divides q - 1.

a. Prove that the polynomial x_n - 1 has n distinct roots in GF(q).

b. Prove that for any finite extension GF(q^m) of GF(q), there exists a primitive element β ∈ GF(q^m) such that {β, β^q, β^{q^2}, . . . , β^{q^m-1}} is a basis for GF(q^m) over GF(q).

c. Now let y be a primitive element of GF(q^mn) such that {γ, γ^q, γ^{q^2}, . . . , γ^{q^nm-1}} is a basis for GF(q^mn) over GF(q). You have proved in part (b) that such an element exists. You have also proved in part (a) that all the n distinct roots of the polynomial xⁿ - 1 lie in in GF(q). Let us denote these roots by e₁, e₂, e₃, . . . , e_n. Define n elements ∝₁, ∝₂, . . . , ∝_n ∈ GF(q^mn) as follows:

 ∝_i =^def γ + (γ^{q^m}/e_i) + (γ^{q^2m}/e_i²) + . . . + (γ^{q^(n-1)m}/e_i^n-1)       for i = 1, 2, . . . , n

Prove that the elements (∝₁)ⁿ, (∝₂)ⁿ, . . . , (∝_n)ⁿ lie in the subfield GF(q^m). That is, show that (∝_i)^{nq^m} = (∝_i)ⁿ for all i = 1, 2, . . . , n.

Hint: First show that this holds for n = 2, with q odd and e₁ = 1, e₂ = -1.

d. Prove that the elements in the set

B =^def {(∝_i)^{q^i} ∈ GF(q^mn) : for i = 1, 2, . . . , n and j = 0, 1, . . . , m - 1}

are linearly independent over GF(q). Therefore, conclude that the set B is a basis for GF(q^mn) as an mn-dimensional vector space over GF(q).

Problem 5: Let C be a binary linear cyclic code of length n with zeros at {∝^Z1, ∝^Z2, . . . , ∝^zr}, where ∝ ∈ GF(2^m) is a primitive n-th root of unity. That is C = (g(x)), where deg g(x) = r and the r roots of g(x) are precisely ∝^Z1, ∝^Z2, . . . , ∝^zr. For any subset I = {i₁, i₂, . . . , i_μ} of {0, 1, . . . , n-1} define the code

C(I) = { (c_i1, c_i2, . . . , c_iμ)   : (c₀, c₁, . . . , c_n-1) with c_i = 0 for all i ∉ I is in C }

In other words, C(I) is the code obtained from C by shortening Cat all the positions that are not in I. Throughout this problem, assume that n = n₁n₂ is an odd composite integer.

a. Write down a parity-check matrix for C(I).

b. Let β ∈ GF(2^m_1) be a primitive n₁-th root of unity, where m₁ is the least integer such that n₁ divides 2^m_1 - 1. Prove that β  ∈ GF(2^m), where m is the least integer such that n divides 2^m - 1.

c. For I = {0, n₂, 2n₂, . . . , (n₁ - 1 )n₂}, show that C(I) is a cyclic code and find the set of zeros of C(I) in terms of {z₁, z₂, . . . ,z_r} and β. In particular, if C is a narrow-sense BCH code of length n₁n₂ = 31·3 = 93 with designed distance 11, express the zeros of C and C(I) as unions of cyclotomic cosets modulo 93 and 31, respectively. What is the dimension of C(I)?

d. Now let C be a BCH code with zeros at ∝⁰, ∝¹, . . . , ∝^δ-1 and their conjugates. Let I₁, I₂ be such that {∝ⁱ : i ∈ I₂}  = {∝^a + ∝ⁱ : i ∈ I₁} for some fixed a. Show that C(I₂) = C(I₁).

Problem 6: Throughout this problem, let BCH(n, q; δ) denote a narrow-sense BCH code of length n with designed distance δ over the finite field GF(q). Further, assume throughout that n and q are relatively prime, and let m denote the least integer such that n divides q^m - 1.

a. Let C be a linear cyclic code of length n over GF(q), and let Z denote the set of zeros of C. That is C = (g(x)), and Z is the set of exponents of all the zeros of g(x). Prove that C contains its dual code C^⊥ if and only if Z ∩ Z^-1 = ∅, where Z^-1 =^def {-z mod n : z ∈ Z}.

b. In this part, assume that n = q - 1. Show that BCH(n, q; δ)^⊥ ⊆ BCH(n, q; δ) if and only if δ ≤ (n+1)/2, where BCH(n, q; δ)^⊥ denotes the dual code of BCH(n, q; δ).

c. Prove that if δ ≥ q√n, then BCH(n, q; δ)^⊥ ? BCH(n, q; δ)

Hint: Express the length n in base q, namely write n = n₀ + n₁q + · · · + n_sq^s for some s.

d. Now let us consider binary BCH codes only. Suppose that n > 2^⌊m/2⌋ and δ ≤ n2^⌊m/2⌋/(2^m - 1). Show that under these conditions, we have

dimBCH(n,2; δ) = n - m ⌈δ-1/2⌉.