1. Let  ∑ ={f0,1}, and let A be the language {abwba| a,b Ε ∑ , w Ε ∑^*}. Construct a DFA that accepts precisely strings in A.

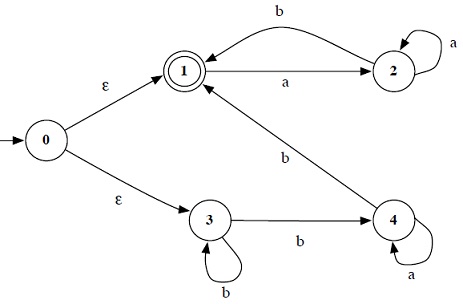
2. Convert the following NFA into an equivalent DFA.

3. (Floyd & Beigel) You and an opponent are seated at a table, and on the table is a square board. At each of the four corners of the board, there is a disc, each one red on one side and black on the other. You are blindfolded, and thus cannot see the con guration of the discs, but you claim that you can ip the discs such that they are all facing with the same color up. On each move, you can ip either one or two discs (either adjacent or diagonal to each other). If this results in a winning state, your opponent must announce that. Otherwise, your opponent may choose to rotate the board 0° , 90° , 180° , or 270° .

Find the shortest sequence of moves that is guaranteed to win the game, no matter what rotations of the board are made. Be sure to include a proof that your solution is correct and that it is the shortest possible.

4. For a language A over an alphabet ∑, define the complement of A, A‾ = {x|x Ε≠ A}. Prove that the class of regular languages is closed under complementation.
5. For a string w = w₁w₂.....w_n, define the reverse of w, w^R = w_n.....w₂w₁. For a language A, define A^R= {w^R |wΕA}. Show that, if A is regular, then so is A^R.

6. For languages A and B, let the shu e of A and B be the language

{w|w = a₁b₁ .....a_kb_k; where a₁.....a_k Ε A and b₁......b_k Ε B; with each a_i,b_i Ε ∑^*} Prove that the class of regular languages is closed under shuffe.

7. Define a 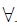FA to be a 5-tuple M = (Q, ∑, δ,q0, F), where δ : QX∑u{Ε}→P(Q) is defined as for a NFA. As a dual notion to nondeterministic acceptance, we say that M accepts x Ε ∑^* if every possible state of M after reading x is an accepting state. Prove that a language is regular if and only if it is recognized by 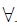a FA.

8. Let M be a NFA with k states.

(a) Prove that, if L(M) ≠ ø;, then L(M) contains a string of length at most k (HINT: Think about the possibilities for path length in M, keeping in mind the Pigeonhole Principle.)

(b) Show that, even if L(M)‾ ≠ ø ;, it is not necessarily the case that L(M)‾ has a string of length at most k.