problem 1: Representing Text and Numbers

A) Latin alphabetic characters can be represented using their ASCII equivalents. prepare the decimal representation of all the characters in “Pei, I.M.” (don’t forget that the punctuation and blank space are considered characters here).

B) UNICODE is a set of numeric values for characters and symbols from around the world. Find the hexadecimal for the Greek letter π (lower case pi) in the table at http://www.unicode.org/charts/

A binary string can mean different things, depending on how it’s interpreted.

C) What decimal number does 01101101 represent if it is interpreted as an unsigned binary number?

D) What ASCII character does the binary string in Problem C represent? You may use the charts at http://www.ascii-code.com

E) What single character does 00011011 00001001 represent in the tables at http://www.unicode.org/charts/?

problem 2: Binary Arithmetic

What is the result of the following 8-bit unsigned binary operations? Give the result in unsigned binary.

A) 00101011 + 01100110

B) 11101000 - 00110101

What is the result of the following 8-bit two’s complement binary operations? Give the result in two’s complement binary.

C) 00110011 + 10011001

D) 11110011 + 10010101

Suppose you have a color represented as a red, green, blue triple, with each component an integer between 0 and 255 represented as an 8-bit unsigned binary number. The red component is 10010011, the green 11111000, and the blue 00001111.

E) What happens if, in an attempt to make the color more red, you add 10000000 to the red component, while leaving the green and blue components as they were?

Convert the following problem into two’s complement binary and perform addition to get the resulting two’s complement binary solution.

F) 80 − 117

problem 3: Logic Tables

Fill in the following logic tables:

A)

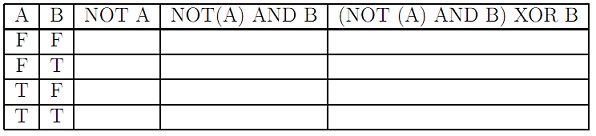
B)

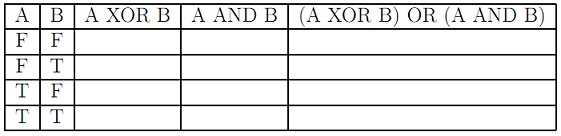
problem 4: Interpreting Logical Statements

View the 2012 list of the 1000 largest US Corporations from Fortune Magazine on the web at http://money.cnn.com/magazines/fortune/fortune500/2012/full list/. This site is linked from the Moodle page so you do not need to retype it. Indicate whether each of the following statements is true or false:

A) Hewlett-Packard has more revenue than Apple, and has more profit than International Business Machines (IBM).

B) If Apple has more profit than Microsoft and Amazon.com has more pro?t than Hewlett-Packard, then Google has more profit than Cisco Systems.

C) Microsoft has more profit than each of the following: Hewlett-Packard, IBM, Dell, Intel, Amazon.com, and Google.

D) Either Cisco Systems has more revenue than Sysco, or Cisco Systems has more profit than Sysco, but not both.

E) If Honeywell International has less revenue than Oracle, then either Microsoft has more profit than Oracle or Apple has more profit than Oracle, but not both.

F) Intel has more revenue than Amazon.com or AT&T has more profit than Microsoft, and it is not the case that both Intel and Microsoft each have more profit than Cisco Systems.

G) Intel and Medtronic both appear on the Top 100 list, or AT&T and Verizon Communications each have more profit than Microsoft.

problem 5: Logic Puzzle

A) Solve the following logic puzzle: You are planning a vacation to Canada with some of your relatives, and you and they vote on which city below to visit. One city got four vote, two got two votes, two got one vote, and the remaining two cities got zero votes. Use logic and the clues below to determine how many votes each city got.

Quebec City
Toronto
Ottawa
Montreal
St. John’s (Newfoundland)
Charlottetown
Halifax

Here are the clues. Make sure you describe how you obtained your answser.

a) Ottawa and Quebec City got different number of votes.
b) Montreal either got the most votes, or it got zero votes.
c) Quebec City got more votes than Halifax did.
d) In the list of cities above, each of the two cities that got two votes has a city that got no votes immediately above it in the list.
e) Either Halifax got one fewer votes than Toronto did, or it got one fewer vote than Ottawa did.

problem 6: Binary and Algorithms

Sometime algorithms work at the bit level. (For ex, serious encryption techniques use a variety of bit-level operations so the encrypted message is difficult to “crack.”) These algorithms are difficult to trace, but doing so is a good exercise in understanding both algorithms and bit operations.

Consider the following algorithm:

BitLogic(a, b)
 Input: two 4-bit binary strings a and b.
 Output: one 4-bit binary string output
1 Set i = 1
2 while i < 4
3 output[i] = b[i + 1]
4 Set i = i + 1
5 Set output[4] = 1
6 Set i = 1
7 while i ≤ 4
8 output[i] = output[i] AND (NOT(a[i]))
9 Set i = i + 1
10 Set tmp = output[4]
11 Set output[4] = output[3]
12 Set output[3] = tmp
13 Print output

Note: In the pseudocode for this problem we use the notation output[i] to mean the value of the ith bit of binary string output, read left to right. So output[1] is the most significant (leftmost) bit and output[4] is the least significant (rightmost) bit, as shown in this figure:

most signi?cant =⇒ least signi?cant
| 1 | 2 | 3 | 4 |
smallest index =⇒ largest index

For ex, if a = 0011, then a[1] = 0 and a[4] = 1. If b = 1010, then b[1] = 1 and b[4] = 0.

A) Trace through the algorithm for input a = 0011, b = 1010. Specifically, (a) show the values of i and output immediately before each time Line 4 is executed, (b) show the values of i and output immediately before each time Line 9 is executed, and (c) show what is printed. In part (a), if a variable is not yet assigned a value when Line 4 is executed, leave the value for that variable blank.

B) Trace through the algorithm for input a = 1001, b = 1111. Specifically, (a) show the values of i and output immediately before each time Line 4 is executed, (b) show the values of i and output immediately before each time Line 9 is executed, and (c) show what is printed. In part (a), if a variable is not yet assigned a value when Line 4 is executed, leave the value for that variable blank.